Question

【题目】综合与实践

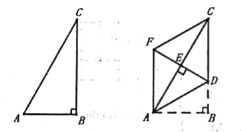
问题情境

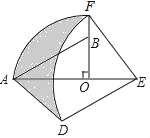
如图1，和均为等边三角形，点，，在同一条直线上，连接；

探究发现

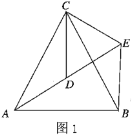
（1）善思组发现：，请你帮他们写出推理过程；

（2）钻研组受善思组的启发，求出了度数，请直接写出等于______度；

（3）奋进组在前面两组的基础上又探索出了与的位置关系为______（请直接写出结果）；

拓展探究

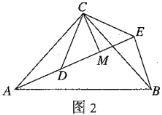
（4）如图2，和均为等腰直角三角形，，点，，在同一条直线上，为中边上的高，连接，试探究，，之间有怎样的数量关系．

创新组类比善思组的发现，很快证出，进而得出．请你写出，，之间的数量关系并帮创新组完成后续的证明过程．

Answer 1

【答案】（1）证明见解析；（2）60；（3）；（4），理由见解析．

【解析】

（1）根据等边三角形的性质可得，，，利用角的和差关系可得，利用SAS可证明；

（2）由外角性质可得∠ADC=120°，根据全等三角形的性质可得∠BEC=∠ADC=120°，进而可得∠AEB的度数；

（3）由∠CDE=∠AEB=60°，即可得出CD//BE；

（4）根据等腰直角三角形的性质可得DE=2CM，根据AD=BE，AE=AD+DE即可得答案．

（1）∵和均为等边三角形，

∴，，，

∴，即：，

在和中，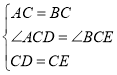

∴

（2）∵△DCE是等边三角形，

∴∠DCE=∠DEC=60°，

∴∠ADC=∠DCE+∠DEC=120°，

由（1）得△ACD≌△BCE，

∴∠ADC=∠BEC=120°，

∴∠AEB=∠BEC-∠DEC=60°，

故答案为：60

（3）∵∠CDE=∠AEB=60°，

∴，

故答案为：CD//BE

（4），证明如下：

∵是等腰直角三角形，

∴，

∵，，

∴，

∴，，

∴，

∴，

∴．