题目内容

如图，A、B是第二象限内双曲线上的点， A、B两点的横坐标分别是a、2a，线段AB的延长线交x轴于点C，若S△AOC=6．则k的值为             （   ▲ ）．

A   6      B.   -6      C.   4       D.   -4
D解析:
分别过点A、B作x轴的垂线，垂足分别为D、E．
则AD∥BE，AD=2BE= ，
∴B、E分别是AC、DC的中点．
∴△ADC∽△BEC，
∵BE：AD=1：2，
∴EC：CD=1：2，
∴EC=DE=a，
∴OC=3a，
又∵A（a， ），B（2a， ），
∴S△AOC= AD×CO=×3a× ==6，
解得：k=4．
双曲线在第二象限，k<0
∴k=-4
故选D．
练习册系列答案
相关题目
今年4月18日，我国铁路第六次大提速，在甲、乙两城市之间开通了动车组高速列车．已知每隔1h有一列速度相同的动车组列车从甲城开往乙城．如图所示，OA是第一列动车组列车离开甲城的路程s（单位：km）与运行时间t（单位：h）的函数图象，BC是一列从乙城开往甲城的普通快车距甲城的路程s（单位：km）与运行时间t（单位：h）的函数图象．请根据图中信息，解答下列问题：
（1）点B的横坐标0.5的意义是普通快车发车时间比第一列动车组列车发车时间
 
h，点B的纵坐标300的意义是
 
；
（2）请你在原图中直接画出第二列动车组列车离开甲城的路程s（单位：km）与时间t（单位：h）的函数图象；
（3）若普通快车的速度为100km/h，
①求BC的解析式，并写出自变量t的取值范围；
②求第二列动车组列车出发后多长时间与普通列车相遇；
③直接写出这列普通列车在行驶途中与迎面而来的相邻两列动车组列车相遇的间隔时间．精英家教网
某汽车公司有豪华和普通两种客车在甲、乙两城市之间运营．已知每隔1小时有一辆豪华客车从甲城开往乙城，如图所示，OA是第一辆豪华客车离开甲城的路程s（单位：千米）与运行时间t（单位：时）的函数图象，BC是一辆从乙城开往甲城的普通客车距甲城的路程s（单位：千米）与运行时间t（单位：时）的函数图象．请根据图中提供的信息，解答下列问题：
（1）点B的横坐标0.5的意义是普通客车发车时间比第一辆豪华客车发车时间
 
小时，点B的纵坐标480的意义是
 
．
（2）请你在原图中直接画出第二辆豪华客车离开甲城的路程s（单位：千米）与运行时间t（单位：精英家教网时）的函数图象．
（3）若普通客车的速度为80千米/时．
①求BC的函数表达式，并写出自变量t的取值范围；
②求第二辆豪华客车出发后多长时间与普通客车相遇；
③直接写出这辆普通客车在行驶途中与迎面而来的相邻两辆豪华客车相遇的间隔时间．
精英家教网如图所示，P是反比例函数图象在第二象限上的一点，且矩形PEOF的面积为3，则反比例函数的表达式是（　　）
A、y=
x
3
B、y=
3
x
C、y=-
3
x
D、y=-
6
x
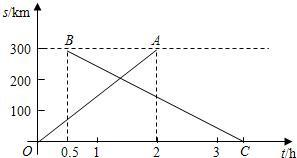
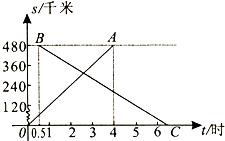宁波与台州两城市之间开通了动车组高速列车．已知每隔1h有一列速度相同的动车组列车从宁波开往台州．如图所示，OA是第一列动车组列车离开宁波的路程s（单位：km）与运行时间t（单位：h）的函数图象，BC是一列从台州开往宁波的普通快车距宁波的路程s（精英家教网单位：km）与运行时间t（单位：h）的函数图象．请根据图中信息，解答下列问题：
（1）点B横坐标0.5的意义是普通快车的发车时间比第一列动车组列车的发车时间晚
 
h，点B的纵坐标300的意义是
 
；
（2）若普通列车的速度为100km/h，
①求BC的解析式；
②求第二列动车组列车出发后多长时间与普通列车相遇．
铁路部门在甲、乙两城市之间开通了动车组高速列车．已知每隔1小时有一列速度相同的动车组列车从甲城开往乙城．如图所示，OA是第一列动车组列车离开甲城的路程s（单位：km）与运行时间t（单位：h）的函数图象，已知该动车组列车的车速是150km/h．BCkm/h是一列速度为100从乙城开往甲城的普通快车距甲城的路程s（单位：km）与运行时间t（单位：h）的函数图象．请根据图中信息，解答下列问题：
（1）请在原坐标系中画出第二列动车组列车离开甲城的路程s（单位：km）与运行时间t（单位：h）的函数图象；
（2）第二列动车组列车出发后多长时间时与普通列车相遇？
（3）普通列车从乙城开往甲城途中，将会遇到多少列从甲城开往乙城的动车组列车（不包括车精英家教网站遇到的情况）？并说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网