题目内容
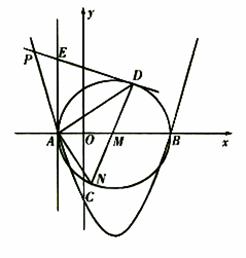
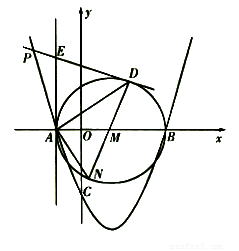
如图所示,抛物线与![]() 轴交于点
轴交于点![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() 以
以![]() 为直径作
为直径作![]() 过抛物线上一点
过抛物线上一点![]() 作
作![]() 的切线
的切线![]() 切点为
切点为![]() 并与
并与![]() 的切线
的切线![]() 相交于点
相交于点![]() 连结
连结![]() 并延长交
并延长交![]() 于点
于点![]() 连结
连结![]()
(1)求抛物线所对应的函数关系式及抛物线的顶点坐标;
(2)若四边形![]() 的面积为
的面积为![]() 求直线
求直线![]() 的函数关系式;
的函数关系式;
 (3)抛物线上是否存在点
(3)抛物线上是否存在点![]() ,使得四边形
,使得四边形![]() 的面积等于
的面积等于![]() 的面积?若存在,求出点
的面积?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
解:(1)因为抛物线与![]() 轴交于点
轴交于点![]() 两点,设抛物线的函数关系式为:
两点,设抛物线的函数关系式为:![]()
∵抛物线与![]() 轴交于点
轴交于点![]()
∴![]()
∴![]()
所以,抛物线的函数关系式为:![]()
又![]()
因此,抛物线的顶点坐标为![]()
(2)连结![]() ∵
∵![]() 是
是![]() 的两条切线,
的两条切线,
∴![]() ∴
∴![]()
又四边形![]() 的面积为
的面积为![]() ∴
∴![]() ∴
∴![]()
又![]() ∴
∴![]()
因此,点![]() 的坐标为
的坐标为![]() 或
或![]()
当![]() 点在第二象限时,切点
点在第二象限时,切点![]() 在第一象限.
在第一象限.
在直角三角形![]() 中,
中,![]()
∴![]() ∴
∴![]()
过切点![]() 作
作![]() 垂足为点
垂足为点![]()
∴![]()
因此,切点![]() 的坐标为
的坐标为![]()
设直线![]() 的函数关系式为
的函数关系式为![]() 将
将![]() 的坐标代入得
的坐标代入得
 解之,得
解之,得
所以,直线![]() 的函数关系式为
的函数关系式为![]()
当![]() 点在第三象限时,切点
点在第三象限时,切点![]() 在第四象限.
在第四象限.
同理可求:切点![]() 的坐标为
的坐标为![]() 直线
直线![]() 的函数关系式为
的函数关系式为![]()
因此,直线![]() 的函数关系式为
的函数关系式为
![]() 或
或![]()
 (3)若四边形
(3)若四边形![]() 的面积等于
的面积等于![]() 的面积
的面积
又![]()
∴![]()
∴![]() 两点到
两点到![]() 轴的距离相等,
轴的距离相等,
∵![]() 与
与![]() 相切,∴点
相切,∴点![]() 与点
与点![]() 在
在![]() 轴同侧,
轴同侧,
∴切线![]() 与
与![]() 轴平行,
轴平行,
此时切线![]() 的函数关系式为
的函数关系式为![]() 或
或![]()
当![]() 时,由
时,由![]() 得,
得,![]()
当![]() 时,由
时,由![]() 得,
得,![]()
故满足条件的点![]() 的位置有4个,分别是
的位置有4个,分别是![]()
![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
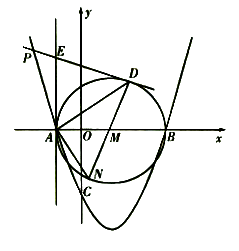
 如图所示,抛物线与x轴交于点A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3).以AB为直径作⊙M,过抛物线上一点P作⊙M的切线PD,切点为D,并与⊙M的切线AE相交于点E,连接DM并延长交⊙M于点N,连接AN、AD.
如图所示,抛物线与x轴交于点A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3).以AB为直径作⊙M,过抛物线上一点P作⊙M的切线PD,切点为D,并与⊙M的切线AE相交于点E,连接DM并延长交⊙M于点N,连接AN、AD. 轴交于点
轴交于点 两点,与
两点,与 轴交于点
轴交于点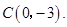 以
以 为直径作
为直径作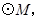 过抛物线上一点
过抛物线上一点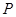 作
作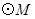 的切线
的切线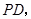 切点为
切点为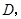 并与
并与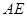 相交于点
相交于点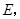 连结
连结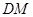 并延长交
并延长交 连结
连结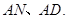
 的面积为
的面积为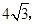 求直线
求直线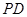 的函数关系式;
的函数关系式;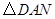 的面积?若存在,求出点
的面积?若存在,求出点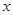 轴交于点
轴交于点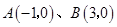 两点,与
两点,与 轴交于点
轴交于点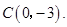 以
以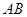 为直径作
为直径作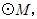 过抛物线上一点
过抛物线上一点 作
作 的切线
的切线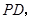 切点为
切点为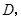 并与
并与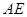 相交于点
相交于点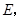 连结
连结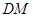 并延长交
并延长交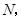 连结
连结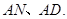
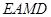 的面积为
的面积为 求直线
求直线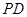 的函数关系式;
的函数关系式;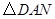 的面积?若存在,求出点
的面积?若存在,求出点