题目内容
(2007•桂林)已知:如图,△ABC关于y轴对称,点B、P关于y轴的对称点分别是点C、Q.BP=AP=2,且P点坐标为(-1,0).(1)分别写出Q点和C点的坐标,并指出△ABP关于y轴的对称三角形;
(2)M为线段CQ上一点,若以x轴为旋转轴,旋转△PAM一周形成的旋转体的全面积为5
 π,求线段AM的长;
π,求线段AM的长;(3)N为线段AM上一动点(与点A、M不重合),过点N分别作NH⊥x轴于H,NG⊥y轴于G.求当矩形OHNG的面积最大时N点的坐标.

【答案】分析:(1)P,Q关于y轴对称,那么Q的坐标应该是(1,0),BP=2,那么CQ=2,因此C的坐标是(3,0),由于B,P关于y轴的对称点分别是C,Q,那么三角形ABP关于y轴的对称三角形就应该是ACQ;
(2)旋转一周得出的图形应该是两个圆锥的组合体,也就是以OA为底面圆半径,AM和AP为母线长的两个圆锥.那么关键是求出OA的长,可在直角三角形AOM中,根据AP,OP的长,求出OA的值,然后根据圆锥体全面积的计算方法表示出圆锥的全面积(这里不应该算底面圆),进而得出AM的值;
(3)求矩形的面积关键是求N点的坐标,那么就必须先求出AM所在直线的解析式,根据直线过A点,我们可将直线设成y=kx+ ,然后根据直线过M点,而OM可以在直角三角形AMO中求出,也就能得出M的坐标,然后用待定系数法求出函数的解析式,这样,可根据矩形的面积公式,以N的横坐标的绝对值当矩形的宽,以N的纵坐标的绝对值当矩形的长,以此可得出关于矩形的面积与横坐标的函数关系式,然后根据函数的性质判定出x为什么值时,矩形的面积最大,然后将x的值代入AM所在直线的解析式中得出N点的坐标.
,然后根据直线过M点,而OM可以在直角三角形AMO中求出,也就能得出M的坐标,然后用待定系数法求出函数的解析式,这样,可根据矩形的面积公式,以N的横坐标的绝对值当矩形的宽,以N的纵坐标的绝对值当矩形的长,以此可得出关于矩形的面积与横坐标的函数关系式,然后根据函数的性质判定出x为什么值时,矩形的面积最大,然后将x的值代入AM所在直线的解析式中得出N点的坐标.
解答:解:(1)Q点坐标为(1,0);C点坐标为(3,0);△ABP与△ACQ关于y轴对称;
(2)在Rt△AOP中,∵AP=2,PO=1,AO= =
= ,依题意有:
,依题意有:
 ×2
×2 π×2+
π×2+ ×2
×2 π×AM=5
π×AM=5 π,∴AM=3;
π,∴AM=3;
(3)在Rt△AOM中,∵AO= ,AM=3,
,AM=3,
∴OM= =
= ,
,
∴点M的坐标为( ,0),设直线AM的解析式为:y=kx+
,0),设直线AM的解析式为:y=kx+ ,
,
∵直线AM经过点M( ,0),
,0), k+
k+ =0,k=-
=0,k=- ,
,
∴直线AM的解析式为:y=- x+
x+ .设点N的坐标为(x,y),
.设点N的坐标为(x,y),
则S矩形AGOH=xy=x(- x+
x+ )=-
)=- x2+
x2+ x=-
x=- (x-
(x- )2+
)2+ ,
,
∴当x= 时,矩形NGOH的面积取得最大值,
时,矩形NGOH的面积取得最大值,
此时y=- x+
x+ =
= ,
,
∴点N的坐标为( ,
, ).
).
点评:本题主要考查了对称的性质,一次函数及二次函数的实际应用等知识点,根据对称得出各边的长是解题的关键.
(2)旋转一周得出的图形应该是两个圆锥的组合体,也就是以OA为底面圆半径,AM和AP为母线长的两个圆锥.那么关键是求出OA的长,可在直角三角形AOM中,根据AP,OP的长,求出OA的值,然后根据圆锥体全面积的计算方法表示出圆锥的全面积(这里不应该算底面圆),进而得出AM的值;
(3)求矩形的面积关键是求N点的坐标,那么就必须先求出AM所在直线的解析式,根据直线过A点,我们可将直线设成y=kx+
 ,然后根据直线过M点,而OM可以在直角三角形AMO中求出,也就能得出M的坐标,然后用待定系数法求出函数的解析式,这样,可根据矩形的面积公式,以N的横坐标的绝对值当矩形的宽,以N的纵坐标的绝对值当矩形的长,以此可得出关于矩形的面积与横坐标的函数关系式,然后根据函数的性质判定出x为什么值时,矩形的面积最大,然后将x的值代入AM所在直线的解析式中得出N点的坐标.
,然后根据直线过M点,而OM可以在直角三角形AMO中求出,也就能得出M的坐标,然后用待定系数法求出函数的解析式,这样,可根据矩形的面积公式,以N的横坐标的绝对值当矩形的宽,以N的纵坐标的绝对值当矩形的长,以此可得出关于矩形的面积与横坐标的函数关系式,然后根据函数的性质判定出x为什么值时,矩形的面积最大,然后将x的值代入AM所在直线的解析式中得出N点的坐标.解答:解:(1)Q点坐标为(1,0);C点坐标为(3,0);△ABP与△ACQ关于y轴对称;
(2)在Rt△AOP中,∵AP=2,PO=1,AO=
 =
= ,依题意有:
,依题意有: ×2
×2 π×2+
π×2+ ×2
×2 π×AM=5
π×AM=5 π,∴AM=3;
π,∴AM=3;(3)在Rt△AOM中,∵AO=
 ,AM=3,
,AM=3,∴OM=
 =
= ,
,∴点M的坐标为(
 ,0),设直线AM的解析式为:y=kx+
,0),设直线AM的解析式为:y=kx+ ,
,∵直线AM经过点M(
 ,0),
,0), k+
k+ =0,k=-
=0,k=- ,
,∴直线AM的解析式为:y=-
 x+
x+ .设点N的坐标为(x,y),
.设点N的坐标为(x,y),则S矩形AGOH=xy=x(-
 x+
x+ )=-
)=- x2+
x2+ x=-
x=- (x-
(x- )2+
)2+ ,
,∴当x=
 时,矩形NGOH的面积取得最大值,
时,矩形NGOH的面积取得最大值,此时y=-
 x+
x+ =
= ,
,∴点N的坐标为(
 ,
, ).
).点评:本题主要考查了对称的性质,一次函数及二次函数的实际应用等知识点,根据对称得出各边的长是解题的关键.

练习册系列答案
相关题目
 π,求线段AM的长;
π,求线段AM的长;
 π,求线段AM的长;
π,求线段AM的长;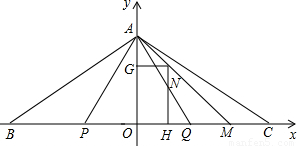
 π,求线段AM的长;
π,求线段AM的长;
 ,土坝与地面的倾角∠ABC=60度,要改造100米长的护坡土坝,选择哪家施工队所需费用较少?
,土坝与地面的倾角∠ABC=60度,要改造100米长的护坡土坝,选择哪家施工队所需费用较少?