题目内容
如果两圆的直径是方程x2-10x+24=0的两根，两圆圆心距为5，则这两个圆的公切线共有（ ）
| A．1条 | B．2条 | C．3条 | D．4条 |
∵x2-10x+24=0，
∴（x-4）（x-6）=0，
解得：x1=4，x2=6，
∵两圆的直径是方程x2-10x+24=0的两根，
∴两圆的直径分别为：4，6，
∴这两圆的半径分别为：2，3，
∵两圆圆心距为5，2+3=5，
∴这两个圆外切，
∴这两个圆的公切线共有3条．
故选C．
∴（x-4）（x-6）=0，
解得：x1=4，x2=6，
∵两圆的直径是方程x2-10x+24=0的两根，
∴两圆的直径分别为：4，6，
∴这两圆的半径分别为：2，3，
∵两圆圆心距为5，2+3=5，
∴这两个圆外切，
∴这两个圆的公切线共有3条．
故选C．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
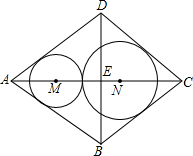形零件（菱形铁片上只能加工同一直径的零件，不计加工过程中的损耗），问加工哪种零件能最充分地利用这种铁片并说明理由．