题目内容
方程|x|(x-1)-k=0有三个不相等的实根.则k的取值范围是( )
分析:首先把原方程变形为|x|(x-1)=k,令y1=|x|(x-1)=
,y2=k,然后作出图形,根据图形得到答案.
|
解答: 解:原方程变形为|x|(x-1)=k,
解:原方程变形为|x|(x-1)=k,
令y1=|x|(x-1)=
,y2=k,
如图,
其图象分别为C1,C2,函数y=x2-x(x≥0)的顶点坐标为(
,-
),
由图象知,当-
<k<0时,直线C2与曲线C1相交,有三个不同的交点.
故选A.
 解:原方程变形为|x|(x-1)=k,
解:原方程变形为|x|(x-1)=k,令y1=|x|(x-1)=
|
如图,
其图象分别为C1,C2,函数y=x2-x(x≥0)的顶点坐标为(
| 1 |
| 2 |
| 1 |
| 4 |
由图象知,当-
| 1 |
| 4 |
故选A.
点评:本题主要考查含绝对值符号的一元二次方程的知识点,解答本题的关键是运用数形结合,此题难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列方程中,以x表示y的是( )
| A、x+y=8 | ||
B、x=
| ||
| C、2y=5x+7 | ||
| D、y=2x-1 |
关于x的分式方程
=
无解,则m的值为( )
| 2x |
| x+1 |
| m |
| x+1 |
| A、-2 | B、-1 | C、0 | D、2 |
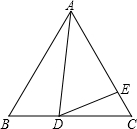 已知:等边△ABC中,AB、cosB是关于x的方程x2-4mx-
已知:等边△ABC中,AB、cosB是关于x的方程x2-4mx-