题目内容
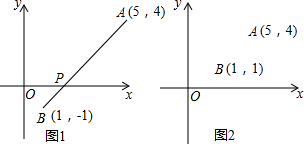
如图(1):点A(5,4),点B(1,-1),在x轴上求一个点P,使PA+PB最小.小芳在思考这个问题时想到两点间线段最短,所以她认为连接AB交x轴与点P,则P是所要求的点.还可以解释如下:在x轴上取另一点M(M不与P点重合),连MA,MB,由三角形的两边之和大于第三边MA+MB一定大于AB,而AB=AP+BP,所以AB与x轴的交点P是所要求的点.
(1)请你求出P点的坐标;
(2)在图(2)中,A(5,4),B(1,1)
①在x轴上求一个点P,使PA+PB最小;
②x轴上能否找到一点Q,使得QA-QB最大?如果能,请在图(3)中画出该点并说明理由;如果不能,请说明理由.
(1)请你求出P点的坐标;
(2)在图(2)中,A(5,4),B(1,1)
①在x轴上求一个点P,使PA+PB最小;
②x轴上能否找到一点Q,使得QA-QB最大?如果能,请在图(3)中画出该点并说明理由;如果不能,请说明理由.

考点:一次函数综合题,轴对称-最短路线问题
专题:
分析:(1)设AB所在的直线对应的函数解析式为y=kx+b,利用待定系数法可求出AB所在的直线对应的函数解析式,再令y=0,可得x的值,即可得出点P的坐标,
(2)①作点B关于x轴的对称点B′,连接AB′交x轴于点P,即是所求点.由(1)即可得出点P的坐标,
②连接AB,并延长AB交x轴与点Q,则QA-QB=AB,在x轴上任取一点N(不与Q重合),则A,B,N三点构成三角形,有NA-NB一定小于AB,所以以上的Q点是所要求的点.
(2)①作点B关于x轴的对称点B′,连接AB′交x轴于点P,即是所求点.由(1)即可得出点P的坐标,
②连接AB,并延长AB交x轴与点Q,则QA-QB=AB,在x轴上任取一点N(不与Q重合),则A,B,N三点构成三角形,有NA-NB一定小于AB,所以以上的Q点是所要求的点.
解答:解:(1)设AB所在的直线对应的函数解析式为:y=kx+b,
把点A(5,4),点B(1,-1)代入得
,解得
,
所以AB所在的直线对应的函数解析式为:y=
x-
,
令y=0,解得x=
,即点P(
,0),
(2)①如图2,作点B关于x轴的对称点B′,连接AB′交x轴于点P,即是所求点.

∵B(1,1),
∴B′(1,-1),
由(1)可得点P(
,0),
②在x轴上能找到一点Q,使得QA-QB最大,
如图3,连接AB,并延长AB交x轴与点Q,则QA-QB=AB,在x轴上任取一点N(不与Q重合),则A,B,N三点构成一个三角形,有NA-NB一定小于AB,
所以以上的Q点是所要求的点.

把点A(5,4),点B(1,-1)代入得
|
|
所以AB所在的直线对应的函数解析式为:y=
| 5 |
| 4 |
| 9 |
| 4 |
令y=0,解得x=
| 9 |
| 5 |
| 9 |
| 5 |
(2)①如图2,作点B关于x轴的对称点B′,连接AB′交x轴于点P,即是所求点.

∵B(1,1),
∴B′(1,-1),
由(1)可得点P(
| 9 |
| 5 |
②在x轴上能找到一点Q,使得QA-QB最大,
如图3,连接AB,并延长AB交x轴与点Q,则QA-QB=AB,在x轴上任取一点N(不与Q重合),则A,B,N三点构成一个三角形,有NA-NB一定小于AB,
所以以上的Q点是所要求的点.

点评:本题主要考查了一次函数的综合题,解题的关键是能理解对称性质及三角形三边关系.

练习册系列答案
相关题目
下列判断错误的是( )
| A、若mx=nx,则m=n | ||||
| B、若x=y,则xm-6=ym-6 | ||||
C、若a=b,则
| ||||
| D、若a=b,则a2=b2 |