题目内容
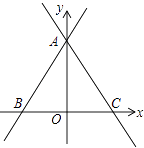
【题目】如图,△ABC中,以BC为直径的圆交AB于点D,∠ACD=∠ABC. 
(1)求证:CA是圆的切线;
(2)若点E是BC上一点,已知BE=6,tan∠ABC= ![]() ,tan∠AEC=
,tan∠AEC= ![]() ,求圆的直径.
,求圆的直径.
【答案】
(1)证明:∵BC是直径,
∴∠BDC=90°,
∴∠ABC+∠DCB=90°,
∵∠ACD=∠ABC,
∴∠ACD+∠DCB=90°,
∴BC⊥CA,∴CA是圆的切线
(2)解:在Rt△AEC中,tan∠AEC= ![]() ,
,
∴ ![]() =
= ![]() ,
,
EC= ![]() AC,
AC,
在Rt△ABC中,tan∠ABC= ![]() ,
,
∴ ![]() =
= ![]() ,
,
BC= ![]() AC,
AC,
∵BC﹣EC=BE,BE=6,
∴ ![]() ,
,
解得:AC= ![]() ,
,
∴BC= ![]() ×
× ![]() =10,
=10,
答:圆的直径是10
【解析】(1)根据圆周角定理BC得到∠BDC=90°,推出∠ACD+∠DCB=90°,即BC⊥CA,即可判断CA是圆的切线;(2)根据锐角三角函数的定义得到tan∠AEC= ![]() ,tan∠ABC=
,tan∠ABC= ![]() ,推出AC=
,推出AC= ![]() EC,BC=
EC,BC= ![]() AC,代入BC﹣EC=BE即可求出AC,进一步求出BC即可.
AC,代入BC﹣EC=BE即可求出AC,进一步求出BC即可.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目