题目内容
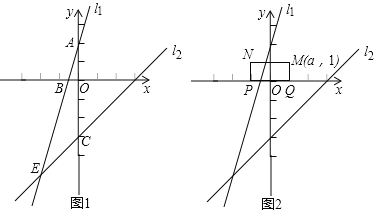
【题目】如图1,在直角坐标系中,一次函数的图象![]() 与
与![]() 轴交于点
轴交于点![]() ,与一次函数
,与一次函数![]() 的图象
的图象![]() 交于点
交于点![]() .
.
(1)求![]() 的值及
的值及![]() 的表达式;
的表达式;
(2)直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与y轴交于点
与y轴交于点![]() ,求四边形
,求四边形![]() 的面积;
的面积;
(3)如图2,已知矩形![]() ,
,![]() ,
,![]() ,
,![]() ,矩形
,矩形![]() 的边
的边![]() 在
在![]() 轴上平移,若矩形
轴上平移,若矩形![]() 与直线
与直线![]() 或
或![]() 有交点,直接写出
有交点,直接写出![]() 的取值范围,
的取值范围,
【答案】(1)![]() ;(2)
;(2)![]()
![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)由点![]() 在一次函数
在一次函数![]() 图象上可求出E点坐标,然后将AE两点坐标代入解析式即可求出l1的表达式;
图象上可求出E点坐标,然后将AE两点坐标代入解析式即可求出l1的表达式;
(2)由于![]() ,求出BC坐标即可解答
,求出BC坐标即可解答
(3)分别求出矩形MNPQ与直线l1或l2有交点边界时的极限值可解答
(1)∵点![]() 在一次函数
在一次函数![]() 图象上,
图象上,
∴![]() ,
,
∴![]() ;
;
设直线![]() 的表达式为
的表达式为![]() ,
,
∵直线![]() 过点
过点![]() 和
和![]() ,
,
∴![]() ,
,
解得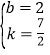 .
.
∴直线![]() 的表达式为
的表达式为![]() .
.
(2)由(1)可知:![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标为
点坐标为![]() ,
,
∴![]()
![]() .
.
(3)![]() 或
或![]() .
.
当Q在直线![]() 上时,a=
上时,a=![]() ,此时矩形MNPQ与直线
,此时矩形MNPQ与直线![]() 有交点a取最小值,
有交点a取最小值,
当N在直线![]() 上时,N点坐标=
上时,N点坐标=![]() ,a=
,a=![]() ,此时矩形MNPQ与直线
,此时矩形MNPQ与直线![]() 有交点a取最大值,
有交点a取最大值,
当Q在直线![]() 上时,a=2,此时矩形MNPQ与直线
上时,a=2,此时矩形MNPQ与直线![]() 有交点a取最小值,
有交点a取最小值,
当N在直线![]() 上时,N点坐标=4,a=6,此时矩形MNPQ与直线
上时,N点坐标=4,a=6,此时矩形MNPQ与直线![]() 有交点a取最大值,
有交点a取最大值,
故当![]() 时,矩形MNPQ与直线
时,矩形MNPQ与直线![]() 有交点,当2≤a≤6时,矩形MNPQ与直线
有交点,当2≤a≤6时,矩形MNPQ与直线![]() 有交点,
有交点,

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案【题目】蔬菜基地种植了娃娃菜和油菜两种蔬菜共![]() 亩,设种植娃娃菜
亩,设种植娃娃菜![]() 亩,总收益为
亩,总收益为![]() 万元,有关数据见下表:
万元,有关数据见下表:
成本(单位:万元/亩) | 销售额(单位:万元/亩) | |
娃娃菜 | 2.4 | 3 |
油菜 | 2 | 2.5 |
(1)求![]() 关于
关于![]() 的函数关系式(收益 = 销售额 – 成本);
的函数关系式(收益 = 销售额 – 成本);
(2)若计划投入的总成本不超过![]() 万元,要使获得的总收益最大,基地应种植娃娃菜和油菜各多少亩?
万元,要使获得的总收益最大,基地应种植娃娃菜和油菜各多少亩?
(3)已知娃娃菜每亩地需要化肥![]() kg,油菜每亩地需要化肥
kg,油菜每亩地需要化肥![]() kg,根据(2)中的种植亩数,基地计划运送所需全部化肥,为了提高效率,实际每次运送化肥的总量是原计划的
kg,根据(2)中的种植亩数,基地计划运送所需全部化肥,为了提高效率,实际每次运送化肥的总量是原计划的![]() 倍,结果运送完全部化肥的次数比原计划少
倍,结果运送完全部化肥的次数比原计划少![]() 次,求基地原计划每次运送多少化肥.
次,求基地原计划每次运送多少化肥.