题目内容
【题目】如图1,反比例函数y= ![]() (x>0)的图象经过点A(2
(x>0)的图象经过点A(2 ![]() ,1),射线AB与反比例函数图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
,1),射线AB与反比例函数图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D. 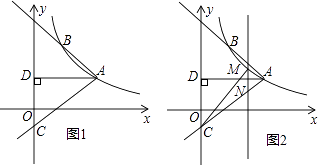
(1)求k的值;
(2)求tan∠DAC的值及直线AC的解析式;
(3)如图2, 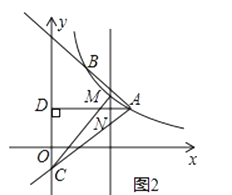
M是线段AC上方反比例函数图象上一动点,过M作直线l⊥x轴,与AC相交于点N,连接CM,求△CMN面积的最大值.
【答案】
(1)解:把A(2 ![]() ,1)代入y=
,1)代入y= ![]()
得k=2 ![]() ×1=2
×1=2 ![]()
(2)解:作BH⊥AD于H,如图1,
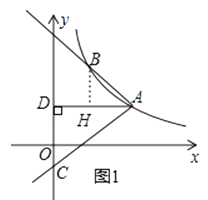
把B(1,a)代入反比例函数解析式y= ![]()
得a=2 ![]() ,
,
∴B点坐标为(1,2 ![]() ),
),
∴AH=2 ![]() ﹣1,BH=2
﹣1,BH=2 ![]() ﹣1,
﹣1,
∴△ABH为等腰直角三角形,
∴∠BAH=45°,
∵∠BAC=75°,
∴∠DAC=∠BAC﹣∠BAH=30°,
∴tan∠DAC=tan30°= ![]() ;
;
∵AD⊥y轴,
∴OD=1,AD=2 ![]() ,
,
∵tan∠DAC= ![]() =
= ![]() ,
,
∴CD=2,
∴OC=1,
∴C点坐标为(0,﹣1),
设直线AC的解析式为y=kx+b,
把A(2 ![]() ,1)、C(0,﹣1)代入
,1)、C(0,﹣1)代入
得 ![]() ,
,
解 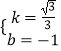 ,
,
∴直线AC的解析式为y= ![]() x﹣1
x﹣1
(3)解:设M点坐标为(t, ![]() )(0<t<2
)(0<t<2 ![]() ),
),
∵直线l⊥x轴,与AC相交于点N,
∴N点的横坐标为t,
∴N点坐标为(t, ![]() t﹣1),
t﹣1),
∴MN= ![]() ﹣(
﹣( ![]() t﹣1)=
t﹣1)= ![]() ﹣
﹣ ![]() t+1,
t+1,
∴S△CMN= ![]() t(
t( ![]() ﹣
﹣ ![]() t+1)
t+1)
=﹣ ![]() t2+
t2+ ![]() t+
t+ ![]()
=﹣ ![]() (t﹣
(t﹣ ![]() )2+
)2+ ![]() (0<t<2
(0<t<2 ![]() ),
),
∵a=﹣ ![]() <0,
<0,
∴当t= ![]() 时,S有最大值,最大值为
时,S有最大值,最大值为 ![]()
【解析】(1)根据反比例函数图象上点的坐标特征易得k=2 ![]() ;(2)作BH⊥AD于H,如图1,根据反比例函数图象上点的坐标特征确定B点坐标为(1,2
;(2)作BH⊥AD于H,如图1,根据反比例函数图象上点的坐标特征确定B点坐标为(1,2 ![]() ),则AH=2
),则AH=2 ![]() ﹣1,BH=2
﹣1,BH=2 ![]() ﹣1,可判断△ABH为等腰直角三角形,所以∠BAH=45°,得到∠DAC=∠BAC﹣∠BAH=30°,根据特殊角的三角函数值得tan∠DAC=
﹣1,可判断△ABH为等腰直角三角形,所以∠BAH=45°,得到∠DAC=∠BAC﹣∠BAH=30°,根据特殊角的三角函数值得tan∠DAC= ![]() ;由于AD⊥y轴,则OD=1,AD=2
;由于AD⊥y轴,则OD=1,AD=2 ![]() ,然后在Rt△OAD中利用正切的定义可计算出CD=2,易得C点坐标为(0,﹣1),于是可根据待定系数法求出直线AC的解析式为y=
,然后在Rt△OAD中利用正切的定义可计算出CD=2,易得C点坐标为(0,﹣1),于是可根据待定系数法求出直线AC的解析式为y= ![]() x﹣1;(3)利用M点在反比例函数图象上,可设M点坐标为(t,
x﹣1;(3)利用M点在反比例函数图象上,可设M点坐标为(t, ![]() )(0<t<2
)(0<t<2 ![]() ),由于直线l⊥x轴,与AC相交于点N,得到N点的横坐标为t,利用一次函数图象上点的坐标特征得到N点坐标为(t,
),由于直线l⊥x轴,与AC相交于点N,得到N点的横坐标为t,利用一次函数图象上点的坐标特征得到N点坐标为(t, ![]() t﹣1),则MN=
t﹣1),则MN= ![]() ﹣
﹣ ![]() t+1,根据三角形面积公式得到S△CMN=
t+1,根据三角形面积公式得到S△CMN= ![]() t(
t( ![]() ﹣
﹣ ![]() t+1),再进行配方得到S=﹣
t+1),再进行配方得到S=﹣ ![]() (t﹣
(t﹣ ![]() )2+
)2+ ![]() (0<t<2
(0<t<2 ![]() ),最后根据二次函数的最值问题求解.
),最后根据二次函数的最值问题求解.
【考点精析】通过灵活运用一次函数的性质和二次函数的最值,掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a即可以解答此题.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案