题目内容
已知，如图，AB是半圆O的直径，点C是半圆上的一点，过点C作CD⊥AB于D，AC=2| 10 |
分析：连接BC，构造直径所对的圆周角是直角，发现直角三角形，根据射影定理求解．
解答：
解：连接BC．
∵AB是半圆O的直径，
∴∠ACB=90°．
∵CD⊥AB，
∴∠ADC=90°．
∴∠ACB=∠ADC．
∵∠A=∠A，
∴△ACD∽△ABC．
∴
=
．
设DB=xcm，则AD=4xcm，AB=5xcm．
∴
=
．
即5x×4x=（2
）2．
解得x=
．
∴AD=4
cm．
解：连接BC．∵AB是半圆O的直径，
∴∠ACB=90°．
∵CD⊥AB，
∴∠ADC=90°．
∴∠ACB=∠ADC．
∵∠A=∠A，
∴△ACD∽△ABC．
∴
| AC |
| AB |
| AD |
| AC |
设DB=xcm，则AD=4xcm，AB=5xcm．
∴
2
| ||
| 5x |
| 4x | ||
2
|
即5x×4x=（2
| 10 |
解得x=
| 2 |
∴AD=4
| 2 |
点评：此题考查了圆周角定理和相似三角形的性质，主要是熟练掌握射影定理．
练习册系列答案
阅读快车系列答案
相关题目
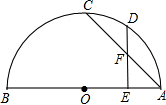已知：如图，AB为⊙O的直径，C、D是半圆弧上的两点，E是AB上除O外的一点，AC与DE相交于F．①
=-
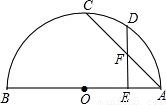
，②DE⊥AB，③AF=DF．
，②DE⊥AB，③AF=DF．
，②DE⊥AB，③AF=DF．