题目内容
 如图所示,四边形ABCD由一个∠ACB=30°的Rt△ABC与等腰Rt△ACD拼成,E为斜边AC的中点,求∠BDE的大小.
如图所示,四边形ABCD由一个∠ACB=30°的Rt△ABC与等腰Rt△ACD拼成,E为斜边AC的中点,求∠BDE的大小.
 解:∵E是Rt△ABC,Rt△ACD斜边AC的中点,
解:∵E是Rt△ABC,Rt△ACD斜边AC的中点,∴BE=DE=
 AC=CE,DE⊥AC,
AC=CE,DE⊥AC,∴∠ACB=∠EBC,∠BDE=∠EBD,
又∵∠ACB=30°,
∴∠AEB=∠EBC+∠ECB=30°+30°=60°
∴∠BED=∠BEA+∠DEA=60°+90°=150°
∴∠BDE=
 (180°-∠BED)=
(180°-∠BED)= (180°-150°)=15°.
(180°-150°)=15°.分析:首先根据E是Rt△ABC,Rt△ACD斜边AC的中点,可得结论BE=DE=
 AC=CE,DE⊥AC,再根据等边对等角可得∠ACB=∠EBC=30°,∠BDE=∠EBD,然后利用角的和差关系计算出∠BED的度数,再根据三角形内角和定理可得到∠BDE的度数.
AC=CE,DE⊥AC,再根据等边对等角可得∠ACB=∠EBC=30°,∠BDE=∠EBD,然后利用角的和差关系计算出∠BED的度数,再根据三角形内角和定理可得到∠BDE的度数.点评:此题主要考查了等腰三角形的性质,以及直角三角形的性质,三角形内角和定理,关键是熟练掌握①在直角三角形中,斜边上的中线等于斜边的一半.②等腰三角形顶角平分线、底边上的高、底边上的中线重合.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 21、如图所示,四边形ABCD是平行四边形,E,F分别在AD,CB的延长线上,且DE=BF,连接FE分别交AB,CD于点H,G.
21、如图所示,四边形ABCD是平行四边形,E,F分别在AD,CB的延长线上,且DE=BF,连接FE分别交AB,CD于点H,G. 12、如图所示,四边形ABCD为⊙O的内接四边形,E为AB延长线的上一点,∠CBE=40°,则∠AOC等于( )
12、如图所示,四边形ABCD为⊙O的内接四边形,E为AB延长线的上一点,∠CBE=40°,则∠AOC等于( )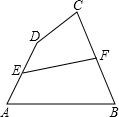 如图所示,四边形ABCD中,E、F分别为AD、BC的中点.
如图所示,四边形ABCD中,E、F分别为AD、BC的中点.
