题目内容
如图，点D、E在△ABC的边BC上，AD=AE，BD=CE，求证：AB=AC．
证明：过点F作AF⊥BC于点F，∵AD=AE，
∴DF=EF，
∵BD=CE，
∴BF=CF，
∴AB=AC．
分析：首先过点F作AF⊥BC于点F，由AD=AE，根据三线合一的性质，可得DF=EF，又由BD=CE，可得BF=CF，然后由线段垂直平分线的性质，可证得AB=AC．
点评：此题考查了等腰三角形的判定与性质．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
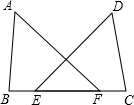如图，点E、F在BC上，AB=DC，∠B=∠C，∠A=∠D，
如图，点C、D在线段AB上，且C为AB的一个四等分点，D为AC中点，若BC=2，则BD的长为