题目内容
在?ABCD中，AB=2，∠B、∠C的平分线分别交AD于点E、F，且EF=1，则BC的长是________．
3
分析：先证△ABE、△CDF是等腰三角形，求出AE，DF的长度，再求AD的长度．
解答：
解：∵AD∥BC，∠B、∠C的平分线分别交AD于点E、F，
∴∠ABE=∠CBE=∠AEB，∠FCD=∠FCB=∠CFD
∴AB=AE=2，CD=DF=2．
∴BC=AB+CD-FE=2AB-EF=3．
故BC的长是3．
故答案为：3．
点评：考查了平行四边对边平行的性质和等腰三角形的性质．
分析：先证△ABE、△CDF是等腰三角形，求出AE，DF的长度，再求AD的长度．
解答：
解：∵AD∥BC，∠B、∠C的平分线分别交AD于点E、F，∴∠ABE=∠CBE=∠AEB，∠FCD=∠FCB=∠CFD
∴AB=AE=2，CD=DF=2．
∴BC=AB+CD-FE=2AB-EF=3．
故BC的长是3．
故答案为：3．
点评：考查了平行四边对边平行的性质和等腰三角形的性质．
练习册系列答案
相关题目
如图所示，在?ABCD中，AB=2AD，∠A=60°，E，F分别为AB，CD的中点，EF=1cm，那么对角线BD的长度为
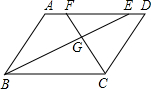如图，在?ABCD中，AB=5，BC=8，∠ABC，∠BCD的角平分线分别交AD于E和F，BE与CF交于点G，则△EFG与△BCG面积之比是（ ）| A、5：8 | B、25：64 | C、1：4 | D、1：16 |
s的速度沿AB向终点B运动，当它们有一个到达终点时，另一个也随之停止运动，设运动时间为ts．