Question

在Rt△ABC中，∠BAC=90°，∠B=30°，线段AD是BC边上的中线．
【小题1】如图(Ⅰ)，将△ADC沿直线BC平移，使点D与点C重合，得到△FCE，连结AF．求证：四边形ADEF是等腰梯形；

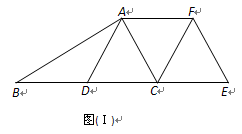
【小题2】如图(Ⅱ)，在（1）的条件下，再将△FCE绕点C顺时针旋转，设旋转角为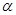（0°<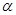<90°）连结AF、DE．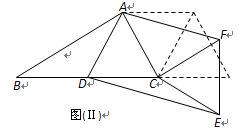

AC⊥CF时，求旋转角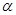的度数；②当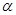=60°时，请判断四边形ADEF的形状，并给予证明．

Answer 1

【小题1】证明：∵△ADC沿直线BC平移得到△FCE，
∴AD∥FC，且AD=FC，∴四边形ADCF是平行四边形，
∴AF∥DC，即AF∥DE，------------------------------------------------1分
∵∠BAC=90°，∠B=30°，∴∠ACD=60°，
∵AD是BC边上的中线，∴AD=DC，-------------------------------2分
∴△ADC是等边三角形，------------------------------------------------3分
∵△ADC≌△FCE，∴△FCE是等边三角形，
∴AD=FE，------------------------------------------------------------------4分
∵AF≠DE，∴四边形ADEF是等腰梯形．--------------------------5分
【小题2】①解：由（1）可知∠1=60°，-----------------6分
当AC⊥CF时，∠2=90°-60°=30°，
∴旋转角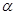的度数为30°，----------------------------------7分
②四边形ADEF为矩形，----------------------------------8分
由（1）可知△ADC和△FCE是全等正三角形，
∴CA=CE=CD=CF，---------------------9分
当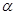=60°时，如图（Ⅲ），∠ACF=60°+60°=120°，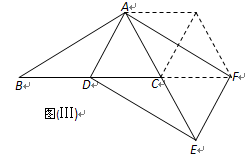

∴∠ACE="120°+60°=180°" ，∴A、C、E三点共线，同理：D、C、F三点共线，--------10分
∴AE=DF，---------11分
∴四边形ADEF为矩形．----------------------12分解析:
利用平移的性质、全等三角形和矩形的判定求证