题目内容
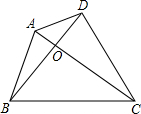 四边形ABCD是任意四边形,AC与BD交点O.求证:AC+BD>
四边形ABCD是任意四边形,AC与BD交点O.求证:AC+BD>| 1 |
| 2 |
证明:在△OAB中有OA+OB>AB
在△OAD中有
OA+OD>AD
OA+OD>AD
,在△ODC中有
OD+OC>CD
OD+OC>CD
,在△
OBC
OBC
中有OB+OC>BC
OB+OC>BC
,∴OA+OB+OA+OD+OD+OC+OC+OB>AB+BC+CD+DA
即:
2(AC+BD)>AB+BC+CD+DA
2(AC+BD)>AB+BC+CD+DA
,即:AC+BD>
| 1 |
| 2 |
分析:直接根据三角形的三边关系进行解答即可.
解答:证明:∵在△OAB中OA+OB>AB
在△OAD中有OA+OD>AD,
在△ODC中有OD+OC>CD,
在△OBC中有OB+OC>BC,
∴OA+OB+OA+OD+OD+OC+OC+OB>AB+BC+CD+DA
即2(AC+BD)>AB+BC+CD+DA,
即AC+BD>
(AB+BC+CD+DA).
故答案为:OA+OD>AD;OD-OC>CD;OBC;OB+OC>BC;2(AC+BD)>AB+BC+CD+DA.
在△OAD中有OA+OD>AD,
在△ODC中有OD+OC>CD,
在△OBC中有OB+OC>BC,
∴OA+OB+OA+OD+OD+OC+OC+OB>AB+BC+CD+DA
即2(AC+BD)>AB+BC+CD+DA,
即AC+BD>
| 1 |
| 2 |
故答案为:OA+OD>AD;OD-OC>CD;OBC;OB+OC>BC;2(AC+BD)>AB+BC+CD+DA.
点评:本题考查的是三角形的三边关系,即三角形任意两边之和大于第三边,任意两边之差小于第三边.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目


 如图,四边形ABCD是任意四边形,过点A,C作BD的平行线,再过点B、D作AC的平行线,设四条直线的交点为P,Q,M,N.
如图,四边形ABCD是任意四边形,过点A,C作BD的平行线,再过点B、D作AC的平行线,设四条直线的交点为P,Q,M,N.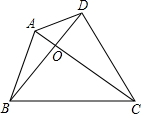 四边形ABCD是任意四边形,AC与BD交点O.求证:AC+BD>
四边形ABCD是任意四边形,AC与BD交点O.求证:AC+BD> (AB+BC+CD+DA).
(AB+BC+CD+DA).