题目内容
已知甲、乙两种原料中均含有A元素,其含量及每吨原料的购买单价如下表所示:
| A元素含量 | 单价(万元/吨) | |
| 甲原料 | 5% | 2.5 |
| 乙原料 | 8% | 6 |
解:设需要甲原料x吨,乙原料y吨.由题意,得

由①,得
y= .
.
把①代入②,得x≤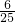 .
.
设这两种原料的费用为W万元,由题意,得
W=2.5x+6y=-1.25x+1.5.
∵k=-1.25<0,
∴W随x的增大而减小.
∴x=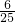 时,W最小=1.2.
时,W最小=1.2.
答:该厂购买这两种原料的费用最少为1.2万元.
分析:设需要甲原料x吨,乙原料y吨.由20千克=0.02吨就可以列出方程5%x+8%y=0.02和不等式5%x×1000x1+8%y×1000x0.5≤16,设购买这两种原料的费用为W万元,根据条件可以列出表达式,由函数的性质就可以得出结论.
点评:本题考查了利用一元一次不等式组和一次函数解决实际问题.解答时列出不等式组,建立一次函数模型并运用一次函数的性质求最值是难点.

由①,得
y=
 .
.把①代入②,得x≤
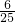 .
.设这两种原料的费用为W万元,由题意,得
W=2.5x+6y=-1.25x+1.5.
∵k=-1.25<0,
∴W随x的增大而减小.
∴x=
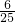 时,W最小=1.2.
时,W最小=1.2.答:该厂购买这两种原料的费用最少为1.2万元.
分析:设需要甲原料x吨,乙原料y吨.由20千克=0.02吨就可以列出方程5%x+8%y=0.02和不等式5%x×1000x1+8%y×1000x0.5≤16,设购买这两种原料的费用为W万元,根据条件可以列出表达式,由函数的性质就可以得出结论.
点评:本题考查了利用一元一次不等式组和一次函数解决实际问题.解答时列出不等式组,建立一次函数模型并运用一次函数的性质求最值是难点.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
已知甲、乙两种原料中均含有A元素,其含量及每吨原料的购买单价如下表所示:
|
|
A元素含量 |
单价(万元/吨) |
|
甲原料 |
5% |
2.5 |
|
乙原料 |
8% |
6 |
已知用甲原料提取每千克A元素要排放废气1吨,用乙原料提取每千克A元素要排放废气0.5吨,若某厂要提取A元素20千克,并要求废气排放不超过16吨,问:该厂购买这两种原料的费用最少是多少万元?
已知甲、乙两种原料中均含有A元素,其含量及每吨原料的购买单价如下表所示:
已知用甲原料提取每千克A元素要排放废气1吨,用乙原料提取每千克A元素要排放废气0.5吨,若某厂要提取A元素20千克,并要求废气排放不超过16吨,问:该厂购买这两种原料的费用最少是多少万元?
| A元素含量 | 单价(万元/吨) | |
| 甲原料 | 5% | 2.5 |
| 乙原料 | 8% | 6 |