Question

【题目】已知，在中，以、为边分别向形外作等边和，为中点，为中点，为中点．

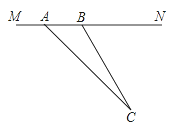
（1）如图(a)所示，当时，的度数为__________．

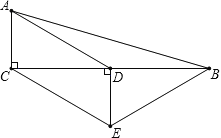
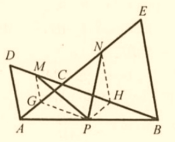
（2）如图(b)所示，当时，的度数是否发生变化？证明你的结论．

Answer 1

【答案】（1）60°；（2）的度数不变，仍是60°，证明见解析．

【解析】

（1）设AC中点G、BC中点H，连接MG、PG；NH，PH，利用中位线定理可以证明△MGP和△PHN全等，然后利用角之间的关系即可得出答案；

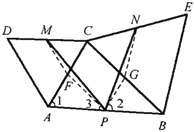
（2）由题意可知MF是等边△ACD的中位线，PG是△ABC的中位线，根据中位线的性质可知四边形CFPG是平行四边形，再根据平行四边形的性质可证明△MFP≌△PGN，即可得出答案.

解：（1）60°

取，的中点分别为，，连接，，，　

又M是CD的中点，P是AB的中点，N是CE的中点

∴MG=AD，MG∥AD，NH=EB，NH∥EB ，GP=BC，GP∥BC ，HP =AC，HP∥AC

又∵△ACD和△ABE均为等边三角形

∴AD=AC，BC=BE，∠MGC=∠DAC=60°，∠CGP=∠ECB=60°, ∠PHC=∠ACD=60°, ∠CHN=∠CBE=60°

∴MG= HP，NH= GP，∠MGP=∠PHN=120°

在△MGP和△PHN中

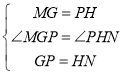
∴△MGP≌△PHN

∴∠MPG=∠PNH

∴∠PNH+∠NPH=180°-∠PHN=60°

（2）的度数不变，仍是60°，

证明：如图所示，取、的中点分别为，，

连接、、、，

∵是等边的中位线，

∴，，

∴．

∵是的中位线，

∴，，

∴，

∴，．

同理，

∴四边形是平行四边形，

∴，

∴，即，

∴，

∴．

∵，

∴．

在中，．

又∵，

∴．

∵，

∴．

∵，，

∴．

又∵，

∴．