题目内容
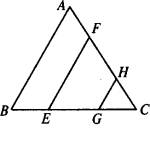
如图,在△ABC中,AB=AC,AD是中线,DE⊥AC于E,F为DE的中点.求证:AF⊥BE. 导析:由等腰三角形的性质知∠ADB=90°,要证AF⊥BE,只需证∠1=∠2,即证△AFD∽△BEC.易知∠ADF=∠BCE,下面只要证明![]() ,这是解决本题的关键.
,这是解决本题的关键.

答案:
解析:
解析:
| 证明:∵AB=AC,AD是中线,∴AD⊥BC.∴∠1+∠3=90º.
∵DE⊥AC,∴∠BCE=∠ADF且△DAC∽△DEC. ∴ ∵F为DE的中点,∴DF= ∴
|

练习册系列答案
相关题目