题目内容
某中学初三(1)(2)两班学生从学校出发,到一山区小学进行“手拉手”活动.初三(1)班学生先出发,行走速度为3km/h;15min后,初三(2)班学生出发,行走速度为3.5km/h.设初三(2)班学生的行走时间为xh.
(1)初三(1)班学生所走的路程y1(km)与x(h)之间的函数关系式为:______,初三(2)班学生所走的路程y2(km)与x(h)之间的函数关系式为:______;
(2)几小时后,初三(2)班的学生赶上初三(1)的学生?
解:(1)y1=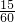 ×3+3x=3x+0.75;y2=3.5x;
×3+3x=3x+0.75;y2=3.5x;
(2)当初三(2)班的学生赶上初三(1)的学生时他们走的路程相等即y1=y2,
∴3x+0.75=3.5x,
∴x=1.5
答:1.5小时后,初三(2)班的学生赶上初三(1)的学生.
分析:(1)根据公式v=st可得到路程y1(km)与x(h)之间的函数关系式和路程y2(km)与x(h)之间的函数关系式;
(2)当初三(2)班的学生赶上初三(1)的学生可得到他们走的路程相等即y1=y2从而求出时间t.
点评:本题考查了一次函数的应用和把一次函数问题转化为一元一次方程的问题.根据题意,找到所求量的等量关系是解决问题的关键.一次函数的一般形式为y=kx+b(k,b是常数,且k≠0).
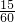 ×3+3x=3x+0.75;y2=3.5x;
×3+3x=3x+0.75;y2=3.5x;(2)当初三(2)班的学生赶上初三(1)的学生时他们走的路程相等即y1=y2,
∴3x+0.75=3.5x,
∴x=1.5
答:1.5小时后,初三(2)班的学生赶上初三(1)的学生.
分析:(1)根据公式v=st可得到路程y1(km)与x(h)之间的函数关系式和路程y2(km)与x(h)之间的函数关系式;
(2)当初三(2)班的学生赶上初三(1)的学生可得到他们走的路程相等即y1=y2从而求出时间t.
点评:本题考查了一次函数的应用和把一次函数问题转化为一元一次方程的问题.根据题意,找到所求量的等量关系是解决问题的关键.一次函数的一般形式为y=kx+b(k,b是常数,且k≠0).

练习册系列答案
相关题目
某中学初三年级的同学参加了一项节能的社会调查活动,为了了解家庭用电的情况,他们随机调查了某地50个家庭一年中生活用电的电费 支出情况,并绘制了如下不完整的频数分布表和频数分布直方图(费用取整数,单位:元).
支出情况,并绘制了如下不完整的频数分布表和频数分布直方图(费用取整数,单位:元).
请你根据以上提供的信息,解答下列问题:
(1)补全频数分布表和频数分布直方图;
(2)若该地区有3万个家庭,请你估计该地区有多少个一年电费支出低于1400元的家庭?
 支出情况,并绘制了如下不完整的频数分布表和频数分布直方图(费用取整数,单位:元).
支出情况,并绘制了如下不完整的频数分布表和频数分布直方图(费用取整数,单位:元).| 分组/元 | 频 数 | 频 率 |
| 1000<x<1200 | 3 | 0.060 |
| 1200<x<1400 | 12 | 0.240 |
| 1400<x<1600 | 18 | 0.360 |
| 1600<x<1800 | 0.200 | |
| 1800<x<2000 | 5 | |
| 2000<x<2200 | 2 | 0.040 |
| 合计 | 50 | 1.000 |
(1)补全频数分布表和频数分布直方图;
(2)若该地区有3万个家庭,请你估计该地区有多少个一年电费支出低于1400元的家庭?
农八师石河子市某中学初三(1)班的学生,在一次数学活动课中,来到市游憩广场,测量坐落在广场中心的王震将军的铜像高度,已知铜像底座的高为3.5m.某小组的实习报告如下,请你计算出铜像的高(结果精确到0.1m).
实习报告2003年9月25日
实习报告2003年9月25日
| 题目1 | 测量底部可以到达的铜像高 | |||
 | ||||
| 测 得 数 据 |
测量项目 | 第一次 | 第二次 | 平均值 |
| BD的长 | 12.3m | 11.7m | ||
| 测倾器CD的高 | 1.32m | 1.28m | ||
| 倾斜角 | α=30°56' | α=31°4' | ||
| 计 算 |
||||
| 结果 | ||||
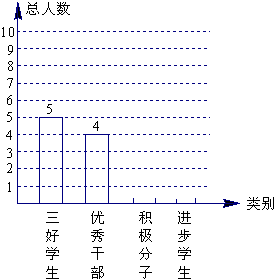 (2011•沙坪坝区模拟)某中学初三年级一、二班优秀学生的情况分布如表:
(2011•沙坪坝区模拟)某中学初三年级一、二班优秀学生的情况分布如表: