题目内容
【题目】今有三部自动换币机，其中甲机总是将一枚硬币换成2枚其他硬币；乙机总是将一枚硬币换成4枚其他硬币；丙机总是将一枚硬币换面10枚其他硬币．某人共进行了12次换币，便将一枚硬币换成了81枚．试问他在丙机上换了_____次？
【答案】8
【解析】
根据题意可知，在甲机上每换一次多1个；在乙机上每换一次多3个；在丙机上每换一次多9个；进行了12次换币就将一枚硬币换成了81枚，多了80个；找到相等关系式列出方程解答即可．
解：设：在甲机换了x次．乙机换了y次．丙机换了z次．
在甲机上每换一次多 1 个；
在乙机上每换一次多 3 个；
在丙机上每换一次多 9 个；
进行了12次换币就将一枚硬币换成了81枚，多了80个；
∴
由②-①，得：2y+8z=68，
∴y+4z=34，
∴y=34-4z，
结合x+y+z=12，能满足上面两式的值为：
∴
；
即在丙机换了8次．
故答案为：8.
练习册系列答案
相关题目
【题目】如图，将一张正方形纸片，剪成四个大小形状一样的小正方形，然后将其中的一个小正方形再按同样的方法剪成四个小正方形，再将其中的一个小正方形剪成四个小正方形，如此循环进行下去；
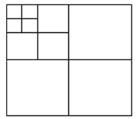
（1）填表
剪的次数 | 1 | 2 | 3 | 4 | 5 |
正方形个数 | 4 | 7 | 10 |
|
|
（2）如果剪n次，共剪出多少个小正方形？
（3）能否经过若干次分割后共得到2019片纸片？若能，请直接写出相应的次数，若不能，请说明理由．
