题目内容
(2011•徐汇区一模)如图,在Rt△ABC中,∠ACB=90°,AB=15,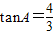 ,E为线AC上一点(不与A、C重合),过点E作EDACED⊥AC交线段AB于点D,将△ADE沿着直线DE翻折,A的对应点G落在射线AC上,线段DG与线段BC交于点M.
,E为线AC上一点(不与A、C重合),过点E作EDACED⊥AC交线段AB于点D,将△ADE沿着直线DE翻折,A的对应点G落在射线AC上,线段DG与线段BC交于点M.(1)若BM=8,求证:EM∥AB;
(2)设EC=x,四边形的ADMC的面积为S,求S关于x的函数解析式,并写出定义域.
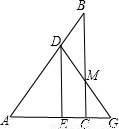
【答案】分析:(1)根据三角函数先在Rt△ACB中,求出AC=9,BC=12,MC=4.再在Rt△MCG中,求出CG=3.可得AG=12,EC=3,AE=6,根据平行线分线段成比例即可证明EM∥AB;
(2)根据SADMC=S△ABC-S△DBM,即可得出S关于x的函数解析式.
解答:解:(1)在Rt△ACB中, ,设AC=3k,BC=4k,(1分)
,设AC=3k,BC=4k,(1分)
则AB= ,AB=5k=15,k=3.
,AB=5k=15,k=3.
∴AC=9,BC=12.(2分)
∵BM=8,
∴MC=4(1分)
在Rt△MCG中, ,
,
∴CG=3.(1分)
∴AG=12,EC=3,AE=6.(1分)
∵ ,
,
∴EM∥AB;(1分)
(2)EC=x,由题意有EG=AE=9-x,则CG=9-2x,(1分)
 ,BM=12-
,BM=12- (9-2x),(1分)
(9-2x),(1分)
SADMC=54- (0<x≤4.5).(3分)
(0<x≤4.5).(3分)
点评:本题综合考查了平行线分线段成比例,三角函数的知识及组合图形的面积之间的关系,函数解析式,有一点的难度.
(2)根据SADMC=S△ABC-S△DBM,即可得出S关于x的函数解析式.
解答:解:(1)在Rt△ACB中,
 ,设AC=3k,BC=4k,(1分)
,设AC=3k,BC=4k,(1分)则AB=
 ,AB=5k=15,k=3.
,AB=5k=15,k=3.∴AC=9,BC=12.(2分)
∵BM=8,
∴MC=4(1分)
在Rt△MCG中,
 ,
,∴CG=3.(1分)
∴AG=12,EC=3,AE=6.(1分)
∵
 ,
,∴EM∥AB;(1分)
(2)EC=x,由题意有EG=AE=9-x,则CG=9-2x,(1分)
 ,BM=12-
,BM=12- (9-2x),(1分)
(9-2x),(1分)SADMC=54-
 (0<x≤4.5).(3分)
(0<x≤4.5).(3分)点评:本题综合考查了平行线分线段成比例,三角函数的知识及组合图形的面积之间的关系,函数解析式,有一点的难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
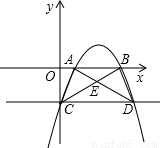
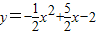 与x轴相交于A、B,与y轴相交于点C,过点C作CD∥x轴,交抛物线点D.
与x轴相交于A、B,与y轴相交于点C,过点C作CD∥x轴,交抛物线点D.