Question

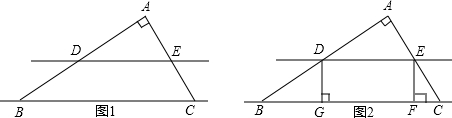
如图1，在Rt△ABC中，∠BAC=90°，AB=80，BC=100．线段BC所在的直线以每秒2个单位的速度沿BA方向运动，并始终保持与原位置平行，交AB于点D，交AC于点E．解答下列问题：
（1）求AC的长．
（2）记x秒时，该直线在△ABC内的部分DE的长度为y，试求出y关于x的函数关系式，并写出自变量x的取值范围．
（3）如图2，过点D作DG⊥BC于点G，过点E作EF⊥BC于点F，当x为何值时，矩形DEFG的面积最大，最大值是多少？

Answer 1

分析：（1）AC的长可由勾股定理直接求解出；
（2）由DE∥BC可得出△ADE∽△ABC，由相似三角形对应边成比例的性质即可求出y与x之间的函数关系式，由AD的长必大于零可确定自变量的取值范围；
（3）通过相似三角形各边的对应关系，可先把要求矩形的面积转化成其中一边的函数，对函数求最值即可．

解答：解：（1）在Rt△ABC中，∠BAC=90°，AB=80，BC=100
∴AC=

BC2-AB2

=

1002-802

=60
即AC的长是60．

（2）根据题意，得：DE∥BC
∴△ADE∽△ABC
∴

DE

BC

=

AD

AB

∵DE=y，AD=AB-BD=80-2x
∴

y

100

=

80-2x

80

（7分）
∴y=-

5

2

x+100（0＜x＜40）

（3）过点A作AM⊥BC于点M，交DE于N点，如图
∵四边形DEFG是矩形
∴DE∥BC
∴△ADN∽△ABM
∴

AN

AM

=

AD

AB

由（2）

DE

BC

=

AD

AB

，得

DE

BC

=

AN

AM

在Rt△ABC中，∠BAC=90°，AM⊥BC
∴S_Rt△ABC=

1

2

•AB•AC=

1

2

•BC•AM
∴AM=

AB•AC

BC

=

80×60

100

=48
AN=AM-MN=48-DG
∴

DE

100

=

48-DG

48

∴DE=-

25

12

DG+100，
∴S_矩形DEFG=DE•DG
=（-

25

12

DG+100）•DG
=-

25

12

DG2+100DG
=-

25

12

（DG²-48DG）
=-

25

12

（DG²-48DG+24²-24²）
=-

25

12

（DG-24）²+1200
∴当DG=24时，矩形DEFG的面积最大，最大值是1200．
∴DE=-

25

12

×12+100=75
由（2）DE=y，y=-

5

2

x+100，得：-

5

2

x+100=75
解得：x=10
经检验：x=10符合题意
综上所述，当x=10时，矩形DEFG的面积最大，最大值1200．

点评：本题考查知识点多，综合性强，是近年来中学数学试题主要的出题形式，要求学生有扎实的相关知识的基本功，及分析问题解决问题的能力．