Question

【题目】如图，O为直线AB上一点，F为射线OC上一点，OE⊥AB．

（1）用量角器和直角三角尺画∠AOC的平分线OD，画FG⊥OC，FG交AB于点G；

（2）在（1）的条件下，比较OF与OG的大小，并说明理由；

（3）在（1）的条件下，若∠BOC＝40°，求∠AOD与∠DOE的度数．

Answer 1

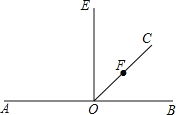
【答案】（1）见解析；（2）OF＜OG；理由见解析；（3）∠AOD＝70°，∠DOE＝20°．

【解析】

（1）使用量角器量出的度数，再用直角三角尺画它的平分线，使用直角三角尺画于G；

（2）根据垂线段最短即可确定OF和OG的大小；

（3）先利用邻补角计算出，再根据角平分线定义得，然后利用角互余计算的度数．

（1）先使用量角器量出的度数，再用直角三角尺画它的平分线；使用直角三角尺画于G，如下图所示，OD、FG即为所画

（2）．理由如下：

是点O到FG的距离

由直线外一点与直线上各点的连线中，垂线段最短可知，；

（3）

∵OD是的平分线

∴

∵

∴

∴

故的度数为，的度数为．