Question

【题目】关于的方程．

求证：无论取任何实数时，方程总有实数根；

当二次函数的图象与轴两个交点的横坐标均为整数，且为负整数时，求出函数的最大（或最小）值，并画出函数图象；

若，是中抛物线上的两点，且，请你结合函数图象确定实数的取值范围．

Answer 1

【答案】(1)详见解析；（2）详见解析；（3）.

【解析】

（1）分类讨论：当k=0时，方程变形一元一次方程，有一个实数解；当k≠0时，计算判别式得到△=(3k-1)2，由此得到△≥0，由此判断当k≠0时，方程有两个实数根；

（2）令y=0，解关于x一元二次方程，求出二次函数图象与x轴的两个交点的横坐标分别为-3和，然后根据整数的整除性可确定负整数k值；

(3)把x=2代入抛物线的解析式即可求出，把x=a代入抛物线的解析式即可用含a的式子表示，再利用即可求出a的取值范围.

解：证明：当时，方程变形为，解得；

当时，，

∵，

∴，

∴当时，方程有实数根，

∴无论取任何实数时，方程总有实数根；

解：

，

解得：，，

所以二次函数的图象与轴两个交点的横坐标分别为和，

根据题意得为整数，且为负整数

所以整数；

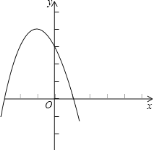
二次函数为；

函数图象如下：

解：把点代入得，

则点的对称点为，

由图象可知：当时，．