题目内容
如图所示,四边形ABCD内接于圆,若AB=AC,且∠ABD=60°.求证:AB=BD+CD.
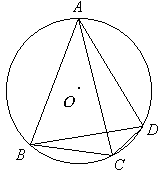
答案:略
解析:
提示:
解析:
|
证法一:延长 CD到E使DE=DB,连接AE,∵四边形ABCD内接于圆,∴∠ADE=∠ABC.
∵ AB=AC,∴∠ABC=∠ADB.∴∠ ADB=∠ADE.在△ADB与△ADE中,
∵∠ABD=∠ACD=60°,∴△ACE是等边三角形. ∴AC=CE,即AB=BD+CD. 证法二:延长BD到F,使DF=CD.∵四边形ABCD内接于圆, ∴∠ABC+∠ADC=180°.∵AB=AC,∴∠ABC=∠ACB=∠ADB. ∵∠ADB+∠ADF=180°,∴∠ADC=∠ADF. △ADC与△ADF中, ∴AC=AF,∴AD=AF.∵∠ABD=60°,∴△ABF是等边三角形. ∴AB=BD+DF,即AB=BD+CD. |
提示:
|
求证的结论是一条线段等于两条线段之和,根据已知条件,四边形 ABCD内接于圆,但是这样的四边形并不都会有这个结论,那么在其中起作用的应是∠ABD=60°及AB=AC.由于AC、BD是对角线,则有∠ABD=∠ACD.又因AB=AC,故问题化为证AC=BD+CD,这时AC与CD相交于点C,且∠ACD=60°,所以这时若能使BD拼接在CD上,再证构成的三角形是等边三角形即可. |

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目

 ∴△ADB≌△ADE,∴AB=AE,∴AC=AE.
∴△ADB≌△ADE,∴AB=AE,∴AC=AE. ∴△ADC≌△ADF,
∴△ADC≌△ADF, 21、如图所示,四边形ABCD是平行四边形,E,F分别在AD,CB的延长线上,且DE=BF,连接FE分别交AB,CD于点H,G.
21、如图所示,四边形ABCD是平行四边形,E,F分别在AD,CB的延长线上,且DE=BF,连接FE分别交AB,CD于点H,G. 12、如图所示,四边形ABCD为⊙O的内接四边形,E为AB延长线的上一点,∠CBE=40°,则∠AOC等于( )
12、如图所示,四边形ABCD为⊙O的内接四边形,E为AB延长线的上一点,∠CBE=40°,则∠AOC等于( )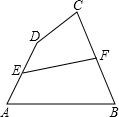 如图所示,四边形ABCD中,E、F分别为AD、BC的中点.
如图所示,四边形ABCD中,E、F分别为AD、BC的中点.
