题目内容
设a、b、c是有理数,满足(3a-2b+c-4)2+(a+2b-3c+6)2+(2a-b+2c-2)2≤0,则2a+b-4c=
- A.-4
- B.

- C.

- D.

A
分析:首先根据已知条件及非负数的性质,得出3a-2b+c-4=0,a+2b-3c+6=0,2a-b+2c-2=0,由此得出a、b、c的值,代入2a+b-4c,计算即可
解答:∵(3a-2b+c-4)2+(a+2b-3c+6)2+(2a-b+2c-2)2≤0,
又∵(3a-2b+c-4)2,≥0,(a+2b-3c+6)2,≥0,(2a-b+2c-2)2≥0,
∴3a-2b+c-4=0,a+2b-3c+6=0,2a-b+2c-2=0,
解得a=- ,b=-
,b=-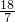 ,c=
,c= .
.
∴2a+b-4c=-4.
故选A.
点评:本题考查了非负数的性质及三元一次方程组的解法,首先根据非负数的性质确定待定的字母的取值,然后代入所求代数式计算即可解决问题.
分析:首先根据已知条件及非负数的性质,得出3a-2b+c-4=0,a+2b-3c+6=0,2a-b+2c-2=0,由此得出a、b、c的值,代入2a+b-4c,计算即可
解答:∵(3a-2b+c-4)2+(a+2b-3c+6)2+(2a-b+2c-2)2≤0,
又∵(3a-2b+c-4)2,≥0,(a+2b-3c+6)2,≥0,(2a-b+2c-2)2≥0,
∴3a-2b+c-4=0,a+2b-3c+6=0,2a-b+2c-2=0,
解得a=-
 ,b=-
,b=-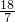 ,c=
,c= .
.∴2a+b-4c=-4.
故选A.
点评:本题考查了非负数的性质及三元一次方程组的解法,首先根据非负数的性质确定待定的字母的取值,然后代入所求代数式计算即可解决问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目