Question

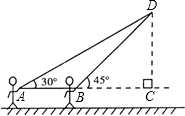（2012•重庆模拟）星期天的上午小明去白塔山玩．如图他在A处时发现白塔顶在D处．此时他测得AD与水平线的夹角为30°． 小明又向前边移动离A处7米的B处，此时他测得BD与水平线的夹角为45°．已知点A、B、C在冋一条直线上，∠ACD=90°．请你求出塔顶D距山脚C多少米？（已知

2

≈1.414，

3

≈1.732．最后结果精确到1米）

Answer 1

分析：先设CD为x米，根据三角函数即可表示出AC于BC的长，再根据AC-BC=AB即可得到一个关于x的方程，解方程即可求得x的值．

解答：解：设CD为x米，
∵∠ACD=90°，
∴在Rt△ADC中，∠DAC=30°，AC=CD•cos30°=

3

x，
在Rt△BCD中，∠DBC=45°，BC=CD=x，
∵AC-BC=AB=7米，
∴

3

x-x=7，
x=

7

3 -1

，
∵

3

≈1.732，
∴x≈10米；
答：塔顶D距山脚C10米．

点评：本题考查了解直角三角形-仰角问题，关键是能借助仰角构造直角三角形列出方程，求出x的值．