题目内容
半径是2和3的两圆交于M、N两点,过交点分别作各圆的切线且相互经过另一个圆的圆心,则公共弦MN之长为
- A.6
- B.12
- C.
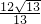
- D.
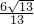
C
分析:根据相交两圆的性质以及切线的判定得出OO′⊥MN,MI=IN,利用三角形面积公式得出MI= 进而求出即可.
进而求出即可.
解答: 解:如图所示:连接MN,
解:如图所示:连接MN,
∵过交点M,N分别作各圆的切线且相互经过另一个圆的圆心,
∴OM⊥O′M,
∵MO=2,MO′=3,
∴OO′=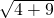 =
= ,
,
由题意可得:OO′⊥MN,MI=IN,
∴MI•OO′=MO•MO′,
∴MI= =
= =
=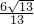 ,
,
∴MN=2×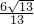 =
=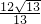 .
.
故选:C.
点评:此题主要考查了相交两圆的性质以及切线的判定等知识,根据已知得出OM⊥O′M是解题关键.
分析:根据相交两圆的性质以及切线的判定得出OO′⊥MN,MI=IN,利用三角形面积公式得出MI=
 进而求出即可.
进而求出即可.解答:
 解:如图所示:连接MN,
解:如图所示:连接MN,∵过交点M,N分别作各圆的切线且相互经过另一个圆的圆心,
∴OM⊥O′M,
∵MO=2,MO′=3,
∴OO′=
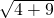 =
= ,
,由题意可得:OO′⊥MN,MI=IN,
∴MI•OO′=MO•MO′,
∴MI=
 =
= =
=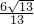 ,
,∴MN=2×
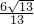 =
=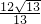 .
.故选:C.
点评:此题主要考查了相交两圆的性质以及切线的判定等知识,根据已知得出OM⊥O′M是解题关键.

练习册系列答案
相关题目

