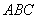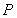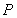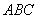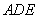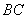题目内容
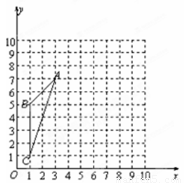
 如图在8×8的正方形网格中建立直角坐标系,已知A(2,4),B(4,2).C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形.
如图在8×8的正方形网格中建立直角坐标系,已知A(2,4),B(4,2).C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形.
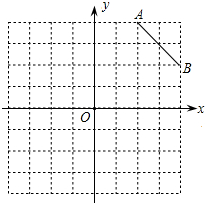
(1)填空:C点的坐标是______,△ABC的面积是______;
(2)将△ABC绕点C旋转360°,求出在旋转过程中线段AB所扫过的面积.
解:(1)
由图形可得符合题意的点C的坐标为(1,1),
S△ABC= AB×CD=
AB×CD= ×2
×2 ×2
×2 =4.
=4.
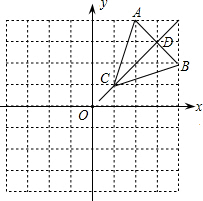
(2)由(1)得,CA= ,CD=2
,CD=2 ,
,
线段AB所扫过的面积为:以C为圆心以BC为半径的圆的面积-以C为圆心以CD为半径的圆的面积,
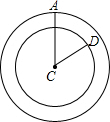
S=10π-8π=2π.
分析:(1)作线段AB的垂直平分线,第一象限内有3个格点,符合条件的只有一个(1,1),再利用面积公式求解即可;
(2)线段AB所扫过的面积是一个圆环的面积,计算出以点C为圆心以BC为半径的圆的面积,以点C为圆心,以CD为半径的圆的面积,相减即可得出答案.
点评:此题考查了勾股定理、等腰三角形的性质及旋转的性质,难点在第二问,关键是分析出线段AB扫过的面积的形状,难度一般.

由图形可得符合题意的点C的坐标为(1,1),
S△ABC=
 AB×CD=
AB×CD= ×2
×2 ×2
×2 =4.
=4.(2)由(1)得,CA=
 ,CD=2
,CD=2 ,
,线段AB所扫过的面积为:以C为圆心以BC为半径的圆的面积-以C为圆心以CD为半径的圆的面积,

S=10π-8π=2π.
分析:(1)作线段AB的垂直平分线,第一象限内有3个格点,符合条件的只有一个(1,1),再利用面积公式求解即可;
(2)线段AB所扫过的面积是一个圆环的面积,计算出以点C为圆心以BC为半径的圆的面积,以点C为圆心,以CD为半径的圆的面积,相减即可得出答案.
点评:此题考查了勾股定理、等腰三角形的性质及旋转的性质,难点在第二问,关键是分析出线段AB扫过的面积的形状,难度一般.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 21、如图在8×8的正方形网格的图形中,有十二棵小树,请你把这个正方形划分成四小块,要求每块的形状、大小都相同,并且每块中恰好有三棵小树,你能行吗?
21、如图在8×8的正方形网格的图形中,有十二棵小树,请你把这个正方形划分成四小块,要求每块的形状、大小都相同,并且每块中恰好有三棵小树,你能行吗? 20、如图在8×8的正方形网格的图形中,有十二棵小树,请你把这个正方形划分成四小块,要求每块的形状、大小都相同,并且每块中恰好有三棵小树,你能行吗?(用红笔画)
20、如图在8×8的正方形网格的图形中,有十二棵小树,请你把这个正方形划分成四小块,要求每块的形状、大小都相同,并且每块中恰好有三棵小树,你能行吗?(用红笔画) 如图在8×8的正方形网格中建立直角坐标系,已知A(2,4),B(4,2).C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形.
如图在8×8的正方形网格中建立直角坐标系,已知A(2,4),B(4,2).C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形.