Question

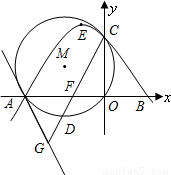
已知：如图，抛物线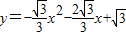的图象与x轴分别交于A，B两点，与y轴交于C点，⊙M经过原点O及点A，C，点D是劣弧OA上一动点（D点与A，O不重合），直线AG切⊙M点A．
（1）求抛物线的顶点E的坐标；
（2）求直线AG的函数解析式；
（3）点D为弧AO的中点，CD交AO于点F，延长CD交AG于点G，求FG的长．

Answer 1

【答案】分析：（1）已知抛物线的解析式，用配方法和公式法求都可以求解；
（2）∵AG是一条直线，利用切线的性质和三角形相似求出与y轴的交点坐标，就可以利用待定系数法求出直线的解析式；
（3）利用弧中点的定义和圆切线的性质求出三角形AFG为正三角形，以及通过解直角三角形求出AF的长而求出FG的长．
解答：解：（1）抛物线y=-x²-
=-（x²+2x+1）+
=-（x+1）²+
∴E的坐标为（-1，）；

（2）连AC，延长AG交y轴于点H；
∵⊙M过A，O，C，且∠AOC=90°，
∴AC为⊙O的直径．当x=0时，y=                    
∴OC=
当y=0时，x₁=-3，x₂=1
∴OA=3，由勾股定理得；
∴AC=2
∵AG是⊙M的切线
∴∠CAG=90°
∴△CAH为直角三角形．
∴△AOC∽△HOA
∴
∴OH=3
∴H（0，-3）
设AG的解析式为：y=kx+b，由题意得
解得：

∴AG的解析式为：．      

（3）在Rt△ACO中，OA=3，OC=，
∵tan∠ACO=．
∴∠ACO=60°，∠CAO=30°．
∵点D是 的中点，
∴．
∴∠ACG=∠DCO=30°．
∴OF=OC•tan30°=1，∠CFO=60°．
∴AF=2，∠AFG=∠CFO=60°，
∵AG是⊙M的切线
∴∠CAG=90°
∴∠FAG=60°
∠FAG=∠AFG=60°
∴△AGF为等边三角形．
∴AG=AF=FG．
∴FG=2．
点评：本题是一道二次函数综合试题，将抛物线与圆放在同一坐标系中研究，因此数形结合的解题思想是不可缺少的，本题考查了相似三角形，切线的性质，待定系数法求函数的解析式，正三角形性质的运用．