题目内容
观察图(1),容易发现图(2)中的∠1=∠2+∠3.把图(2)推广到图(3),其中有8个角:∠1,∠2,…,∠8.可以验证∠1=∠2+∠5+∠8成立.除此之外,恰好还有一组正整数x,y,z,满足2≤x≤y≤z≤8,使得∠1=∠x+∠y+∠z,那么这组正整数(x,y,z)=( )


分析:利用三角形外角的性质及边长为1的正方形网格的性质得到和等于45°的3个角的即可得到答案.
解答:解:∵小正方形的边长为1,
∴∠1=45°,
∵∠1=∠x+∠y+∠z,
∴x+y+z=45,
∵一组正整数x,y,z,满足2≤x≤y≤z≤8,
∴∠1=∠3+∠4+∠7=45°,
∴这组正整数(x,y,z)=3,4,7;
故选A.
∴∠1=45°,
∵∠1=∠x+∠y+∠z,
∴x+y+z=45,
∵一组正整数x,y,z,满足2≤x≤y≤z≤8,
∴∠1=∠3+∠4+∠7=45°,
∴这组正整数(x,y,z)=3,4,7;
故选A.
点评:本题考查了图形规律类题目,解题的关键是仔细地观察题目提供的例子并从中找到正确的规律,并利用此规律解题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
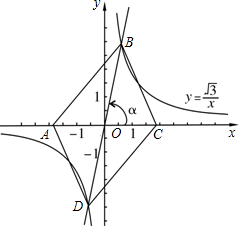 我们容易发现:反比例函数的图象是一个中心对称图形.你可以利用这一结论解决问题.如图,在同一直角坐标系中,正比例函数的图象可以看作是:将x轴所在的直线绕着原点O逆时针旋转α度角后的图形.若它与反比例函数
我们容易发现:反比例函数的图象是一个中心对称图形.你可以利用这一结论解决问题.如图,在同一直角坐标系中,正比例函数的图象可以看作是:将x轴所在的直线绕着原点O逆时针旋转α度角后的图形.若它与反比例函数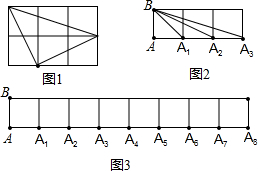 (∠AA1B简写做∠i)观察图1,容易发现图2中的∠1=∠2+∠3.把图2推广到图3,其中有8个角:∠1,∠2,∠3,…,∠8.可以验证∠1=∠2+∠5+∠8成立.除此之外,恰好还有一组正整数x,y,z,满足2≤x≤y≤z≤8,使得∠1=∠x+∠y+∠z,那么这组正整数(x,y,z)=
(∠AA1B简写做∠i)观察图1,容易发现图2中的∠1=∠2+∠3.把图2推广到图3,其中有8个角:∠1,∠2,∠3,…,∠8.可以验证∠1=∠2+∠5+∠8成立.除此之外,恰好还有一组正整数x,y,z,满足2≤x≤y≤z≤8,使得∠1=∠x+∠y+∠z,那么这组正整数(x,y,z)= .
.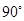 ,那么按方案三所焊接成的大扇形的圆心角也为
,那么按方案三所焊接成的大扇形的圆心角也为 (∠AA1B简写做∠i)观察图1,容易发现图2中的∠1=∠2+∠3.把图2推广到图3,其中有8个角:∠1,∠2,∠3,…,∠8.可以验证∠1=∠2+∠5+∠8成立.除此之外,恰好还有一组正整数x,y,z,满足2≤x≤y≤z≤8,使得∠1=∠x+∠y+∠z,那么这组正整数(x,y,z)=________.
(∠AA1B简写做∠i)观察图1,容易发现图2中的∠1=∠2+∠3.把图2推广到图3,其中有8个角:∠1,∠2,∠3,…,∠8.可以验证∠1=∠2+∠5+∠8成立.除此之外,恰好还有一组正整数x,y,z,满足2≤x≤y≤z≤8,使得∠1=∠x+∠y+∠z,那么这组正整数(x,y,z)=________.