Question

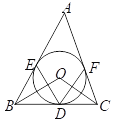
【题目】如图，以△ABC的边AC为直径作⊙O交AB、BC于E、D，D恰为BC的中点，过C作⊙O的切线，与AB的延长线交于F，过B作BM⊥AF，交CF于M．

（1）求证：MB＝MC；

（2）若MF＝5，MB＝3，求⊙O的半径及弦AE的长．

Answer 1

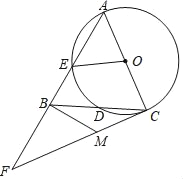
【答案】（1）见解析；（2）EA＝

【解析】

（1）连接AD，根据垂直平分线的判定和切线的性质证明即可；

（2）根据相似三角形的判定和性质解答即可．

（1）证明：连接AD，∵AC是⊙O的直径，

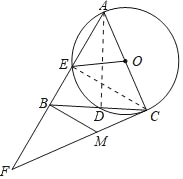
∴∠ADC＝90°，

∠ADB＝90°，又D是BC的中点，

∴AD是线段BC的垂直平分线，

∴AB＝AC，∠ABC＝∠ACB，

∵BM⊥AF，CF是⊙O的切线，

∴∠ABM＝∠ACM＝90°，

∴∠MBC＝∠MCB，MB＝MC；

（2）∵MF＝5，MB＝3，

∴FB＝4，由上知MC＝3，FC＝8，

∵∠MBF＝∠ACF＝90°，∠BFM＝∠CFA，

∴△FBM∽△FCA，

∴，

即，

解得：CA＝6，⊙O的半径OA＝3，

连结CE，则∠AEC＝90°，由上知，∠F＝∠ACE，则△EAC∽△BMF，

∴

解得：EA＝