题目内容
如图，在⊙O中，直径CD与弦AB相交于点E，若BE=3，AE=4，DE=2，则⊙O的半径是
- A.3
- B.4
- C.6
- D.8
B
分析：利用相交弦定理，可以求出CE的长，从而知道CD的长，就可求出⊙O的半径．
解答：根据相交弦定理，AE•BE=CE•DE，
又∵BE=3，AE=4，DE=2，
∴CE=6
∴CD=CE+DE=8
那么圆的半径等于4．
故选B．
点评：此题考查了相交弦定理，先求出直径，再得出半径．
分析：利用相交弦定理，可以求出CE的长，从而知道CD的长，就可求出⊙O的半径．
解答：根据相交弦定理，AE•BE=CE•DE，
又∵BE=3，AE=4，DE=2，
∴CE=6
∴CD=CE+DE=8
那么圆的半径等于4．
故选B．
点评：此题考查了相交弦定理，先求出直径，再得出半径．
练习册系列答案
导学全程练创优训练系列答案
相关题目
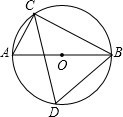如图，在⊙O中，直径AB为10cm，弦AC为6cm，∠ACB的平分线交⊙O于D，则BC=
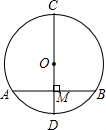如图，在⊙O中，直径CD的长度为10cm，AB是弦，且AB⊥CD于M，OM=3cm，求弦AB的长．
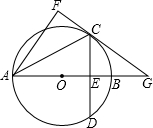C与直线AB相交于点G．
（2013•百色）如图，在⊙O中，直径CD垂直于弦AB，若∠C=25°，则∠ABO的度数是（ ）
（2012•朝阳区二模）如图，在⊙O中，直径AB⊥弦CD于点H，E是⊙O上的点，若∠BEC=25°，则∠BAD的度数为（ ）