题目内容
如图，一人工湖的对岸有一条笔直的小路，湖上原有一座小桥与小路垂直相通，现小桥有一部分已断裂，另一部分完好． 站在完好的桥头A测得路边的小树D在它的北偏西30°，向正北方向前进32米到断口B处，又测得小树D在它的北偏西45°，请计算小桥断裂部分的长．（| 3 |
分析：在本题中有两个直角三角形，且有公共边，利用已知角的正切值，构建边之间的方程关系，解答即可．
解答：
解：依题意，延长AB交小路于C点，设BC=x
∵∠CBD=45°，AC⊥DC
∴BC=CD=x
在Rt△ADC中∠DAC=30°，AB=32，
∴AC=x+32
∴tan30°=
即：
=
解得x≈44米…（4分）
答：断裂部分的长约为44米．
解：依题意，延长AB交小路于C点，设BC=x∵∠CBD=45°，AC⊥DC
∴BC=CD=x
在Rt△ADC中∠DAC=30°，AB=32，
∴AC=x+32
∴tan30°=
| CD |
| AC |
即：
| ||
| 3 |
| x |
| x+32 |
解得x≈44米…（4分）
答：断裂部分的长约为44米．
点评：本题考查了解直角三角形的应用，解一般三角形，求三角形的边或高的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线．
练习册系列答案
相关题目
如图，一人工湖的对岸有一条笔直的小路，湖上原有一座小桥与小路垂直相通，现小桥有一部分已经断裂，另一部分完好，站在完好部分的桥头A测得路边小树D在它的北偏西30°，前进32米的断口B处，又测得小树D在它的北偏西45°，则小桥断裂部分的长为
如图，一人工湖的对岸有一条笔直的小路，湖上原有一座小桥与小路垂直相通，现小桥有一部分已断裂，另一部分完好． 站在完好的桥头A测得路边的小树D在它的北偏西30°，向正北方向前进32米到断口B处，又测得小树D在它的北偏西45°，请计算小桥断裂部分的长．（
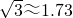，结果保留整数）
，结果保留整数）