题目内容
【题目】如图，在平面直角坐标系中，点A、B、C、E、P均在坐标轴上，A（0，3）、B（﹣4，0）、P（0，﹣3），点C是线段OP（不包含O、P）上一动点，AB∥CE，延长CE到D，使CD=BA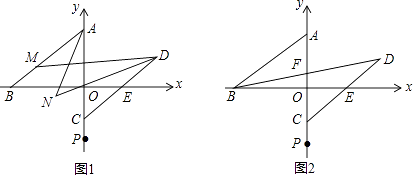
（1）如图，点M在线段AB上，连MD，∠MAO与∠MDC的平分线交于N．若∠BAO=α，∠BMD=130°，则∠AND的度数为
（2）如图，连BD交y轴于F．若OC=2OF，求点C的坐标
（3）如图，连BD交y轴于F，在点C运动的过程中， 
的值是否变化？若不变，求出其值；若变化，请说明理由．
【答案】
（1）
α+25°
（2）
解：如图2中，
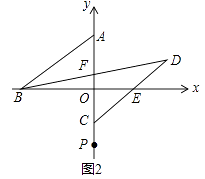
∵AB∥CD，
∴△AFB∽△CFD，
∴ 
= 
，∵AB=CD，
∴AF=FC，
∵OC=2OF，设OF=a，则OC=2a，FC=AF=3a，OA=4a，
∴4a=3，
∴a= 
，
∴OC=2a= 
，
∴C（0，﹣ ）
（3）
解：结论： 
的值不变．理由如下：
如图2中，∵AB∥CD，
∴△AFB∽△CFD，
∴ = ，∵AB=CD，
∴AF=FC，设OF=m，则AF=3﹣m，OC=3﹣m﹣m=3﹣2m，
∴ = 
= 
=2，
∴ 的值不变
【解析】解：（1）如图1中，作NG∥AB．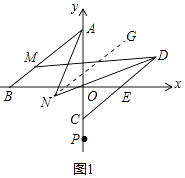
∵AB∥CD，NG∥AB，
∴AB∥NG∥CD，
∴∠ANG=∠BAN，∠DNG=∠NDC，
∵∠NAB= ∠BAO，∠NDC= ∠MDC，
∴∠AND=∠ANG+∠DNG= ∠BAO+ ∠MDC，
∵∠BAO=α，∠MDC=180°﹣∠BMD=180°﹣130°=50°，
∴∠AND= α+25°，
所以答案是 α+25°；
【考点精析】关于本题考查的角平分线的性质定理和相似三角形的判定与性质，需要了解定理1：在角的平分线上的点到这个角的两边的距离相等； 定理2：一个角的两边的距离相等的点，在这个角的平分线上；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方才能得出正确答案．
