题目内容
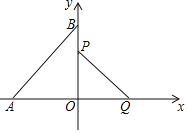
【题目】如图,在直角坐标系中,点A、B分别在x轴和y轴上,△OBA是等腰直角三角形且AB=![]() ,线段PQ=1,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动.
,线段PQ=1,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动.
(1)求A、B两点的坐标;
(2)若P运动的路程为m,△OPA的面积为S,求S与m之间的函数关系式;
(3)当点P运动一周时,点Q运动的总路程为______.
【答案】(1)A点的坐标为:(-1,0),B点的坐标为:(0,1);(2)S与m之间的函数关系式为S=![]() m(0<m≤1),或S=
m(0<m≤1),或S=![]() +
+![]() -
-![]() m(1<m<
m(1<m<![]() +1);(3)2
+1);(3)2![]() .
.
【解析】
(1)由△OBA是等腰直角三角形且AB=![]() ,得出OA=OB=1,即可得出A、B两点的坐标;(2)分三种情况讨论:①当点P在OB边上时,由三角形面积公式即可得出结果;②当点P在AB边上时,作PD⊥OA于D,△APD是等腰直角三角形,则PB=m-1,求出AP的长,由等腰直角三角形的性质得出PD的长,由三角形面积公式即可得出结果;③当点P在AO边上时,△OPA不存在;(3)根据题意正确画出从O→B→A运动一周的图形,分四种情况进行计算:①点P从O→B时,路程是线段PQ的长;②当点P从B→C时(QC⊥AB,C为垂足),点Q从O运动到Q,计算OQ的长就是运动的路程;③点P从C→A时,点Q由O向左运动,路程为QO;④点P从A→O时,点Q运动的路程就是点P运动的路程;最后相加即可.
,得出OA=OB=1,即可得出A、B两点的坐标;(2)分三种情况讨论:①当点P在OB边上时,由三角形面积公式即可得出结果;②当点P在AB边上时,作PD⊥OA于D,△APD是等腰直角三角形,则PB=m-1,求出AP的长,由等腰直角三角形的性质得出PD的长,由三角形面积公式即可得出结果;③当点P在AO边上时,△OPA不存在;(3)根据题意正确画出从O→B→A运动一周的图形,分四种情况进行计算:①点P从O→B时,路程是线段PQ的长;②当点P从B→C时(QC⊥AB,C为垂足),点Q从O运动到Q,计算OQ的长就是运动的路程;③点P从C→A时,点Q由O向左运动,路程为QO;④点P从A→O时,点Q运动的路程就是点P运动的路程;最后相加即可.
(1)∵△OBA是等腰直角三角形且AB=![]() ,
,
∴OA=OB=1,
∴A点的坐标为:(-1,0),B点的坐标为:(0,1);
(2)分三种情况讨论:
①当点P在OB边上,即0<m≤1时,如图1所示:
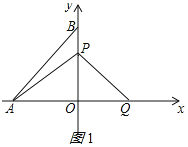
△OPA的面积S=![]() OA×OP=
OA×OP=![]() ×1×m=
×1×m=![]() m;
m;
②当点P在AB边上,即1<m<![]() +1时,如图2所示:
+1时,如图2所示:
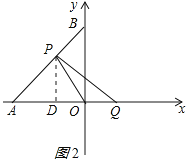
作PD⊥OA于D,△APD是等腰直角三角形,
∵PB=m-1,
∴AP=AB-PB=![]() -(m-1)=
-(m-1)=![]() +1-m,
+1-m,
∴PD=![]() AP=
AP=![]() (
(![]() +1-m)=1+
+1-m)=1+![]() -
-![]() m,
m,
∴△OPA的面积=![]() OA×PD=
OA×PD=![]() ×1×(1+
×1×(1+![]() -
-![]() m)=
m)= ![]() +
+![]() -
-![]() m,即S=
m,即S=![]() +
+![]() -
-![]() m;
m;
③当点P在AO边上,即![]() +1≤m≤
+1≤m≤![]() +2时,△OPA不存在;
+2时,△OPA不存在;
综上所述,S与m之间的函数关系式为S=![]() m(0<m≤1),或S=
m(0<m≤1),或S=![]() +
+![]() -
-![]() m(1<m<
m(1<m<![]() +1);
+1);
(3)∵△OBA是等腰直角三角形,
∴∠ABO=∠BAO=45°,
∵OA=OB=1,PQ=1,
①当点P从O→B时,点Q运动的路程为PQ的长,即为1;
②如图3所示,QC⊥AB,则∠ACQ=90°,即PQ运动到与AB垂直时,垂足为P,
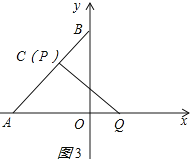
当点P从B→C时,
∵∠ABO=∠BAO=45°,
∴∠OQC=90°-45°=45°,
∴AQ=![]() PQ=
PQ=![]() ,
,
∴OQ=AQ-OA=![]() -1,
-1,
则点Q运动的路程为QO=![]() -1;
-1;
③当点P从C→A时,点Q运动的路程为QO=![]() -1;
-1;
④当点P从A→O时,点Q运动的路程为AO=1,
∴点Q运动的总路程为:1+![]() -1+
-1+![]() -1+1=2
-1+1=2![]() ;
;
故答案为:2![]() .
.

【题目】某环保小组为了解世博园的游客在园区内购买瓶装饮料数量的情况,一天,他们分别在A、B、C三个出口处,对离开园区的游客进行调查,其中在A出口调查所得的数据整理后绘成如下图所示统计图:
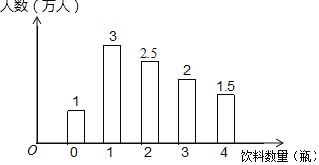
(1)在A出口的被调查游客中,购买瓶装饮料的数量的中位数是______瓶、众数是______瓶、平均数是______瓶;
(2)已知A、B、C三个出口的游客量比为2:2:1,用上面图表的人均购买饮料数量计算:这一天景区内若有50万游客,那么这一天购买的饮料的总数是多少?
表一:
出口 | B | C |
人均购买饮料数量(瓶) | 3 | 2 |
(3)若每瓶饮料要消耗0.5元处理包装的环保费用,该日需要花费多少钱处理这些饮料瓶?由此请你对游客做一点环保宣传建议.