题目内容
（本题满分6分）等腰△ABC，AB=AC=８，∠BAC=120°，P为BC的中点，小亮拿着300角的透明三角板，使300角的顶点落在点P，三角板绕P点旋转．
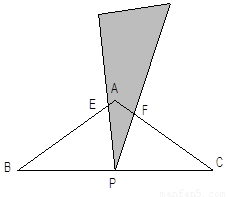
（1）如图a，当三角板的两边分别交AB、AC于点E、F时．求证：△BPE∽△CFP；
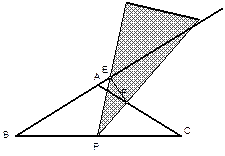
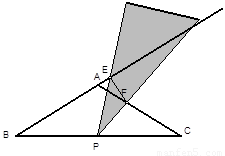
（2）操作：将三角板绕点P旋转到图b情形时，三角板的两边分别交BA的延长线、边AC于点E、F．
①探究１：△BPE与△CFP还相似吗？
②探究２：连结EF，△BPE与△PFE是否相似？请说明理由；
③设EF=m，△EPF的面积为S，试用m的代数式表示S．
解：（1）证明：
而
所以
由
可知
结论成立. ………………………………………………………………………（3分）
（2）相似……………………………………………………………………………（4分）
‚相似……………………………………………………………………………（5分）
理由：由△BPE与△CFP相似可得
即
，而 知结论成立…………（6分）
③由△BPE与△PFE相似得
，即
，过F作PE垂线可得
………………………………………………（7分）
解析:略
练习册系列答案
名校课堂系列答案
相关题目
