题目内容
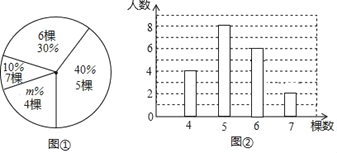
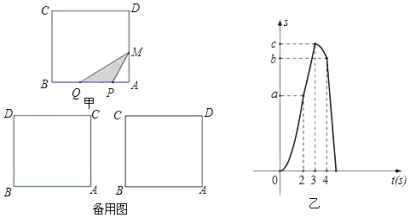
【题目】如图甲，在正方形ABCD中，AB＝6cm，点P、Q从A点沿边AB、BC、CD运动，点M从A点沿边AD、DC、CB运动，点P、Q的速度分别为1cm/s，3cm/s，点M的速度2cm/s．若它们同时出发，当点M与点Q相遇时，所有点都停止运动．设运动的时间为ts，△PQM的面积为Scm2，则S关于t的函数图象如图乙所示．结合图形，完成以下各题：
（1）填空：a＝ ；b＝ ；c＝ ．
（2）当t为何值时，点M与点Q相遇？
（3）当2＜t≤3时，求S与t的函数关系式；
（4）在整个运动过程中，△PQM能否为直角三角形？若能，请求出此时t的值；若不能，请说明理由．
【答案】解：⑴ 根据题意可列方程为
，则
答：当时，点M与点Q相遇。---------------------------------3分
⑵ 8；13.5；12（每空1分）
(3)当
时,
Ｓ与t的函数关系式是
=
-----------------------------------------------------------------------------------9分
(4) 当0＜t≤2时，
不能成为直角三角形；
当时，若能成为直角三角形，则有△BPQ∽△CMP，即
，可求出
；
当3＜t≤4时，若能成为直角三角形，则有△BPQ∽△AQM，即
，无解；
当4＜t＜4．8时，
，
----------------------------------------------------------------12分
【解析】
（1）根据题意列出方程2t+3t=4×6求解即可；
（2）分别令时间t为2、3、4求得相应的三角形的面积即为a、b、cd的值；
（3）当2＜t≤3时即点P、Q在线段AB上运动时，表示出该三角形的面积即可；
（4）分0＜t≤2、2＜t≤3、2＜t≤3、4＜t＜4.8四种情况讨论．
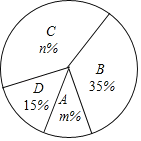
【题目】今年5月份，我市某中学开展争做“五好小公民”征文比赛活动，赛后随机抽取了部分参赛学生的成绩，按得分划分为A，B，C，D四个等级，并绘制了如下不完整的频数分布表和扇形统计图：
等级 | 成绩（s） | 频数（人数） |
A | 90＜s≤100 | 4 |
B | 80＜s≤90 | x |
C | 70＜s≤80 | 16 |
D | s≤70 | 6 |
根据以上信息，解答以下问题：
（1）表中的x= ；
（2）扇形统计图中m= ，n= ，C等级对应的扇形的圆心角为 度；
（3）该校准备从上述获得A等级的四名学生中选取两人做为学校“五好小公民”志愿者，已知这四人中有两名男生（用a1，a2表示）和两名女生（用b1，b2表示），请用列表或画树状图的方法求恰好选取的是a1和b1的概率．
