Question

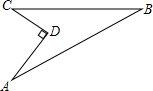
△ABC中，AB=5，AC=4

2

，BC边上的高AD=4，则BC=______．

Answer 1

（1）AB=5，AC=4

2

，BC边上的高AD=4，
在Rt△ABD中AB=5，AD=4，由勾股定理得
BD²=AB²-AD²，
∴BD=3，
在Rt△ACD中AC=4

2

，AD=4，由勾股定理得
CD²=AC²-AD²，
∴CD=3，
∴BC的长为BD+DC=7；
（2）钝角△ABC中，AB=5，AC=4

2

，BC边上高AD=4，
在Rt△ABD中AB=5，AD=4，由勾股定理得
BD²=AB²-AD²=13²-12²=25，
∴BD=4，
在Rt△ACD中AC=4

2

，AD=4，由勾股定理得
CD²=AC²-AD²，
∴CD=3，
∴BC的长为DC-BD=1．
故答案为7或1．