��Ŀ����
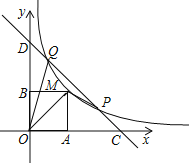
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�����y=![]() ��mΪ������m��1��x��0����ͼ����P��m��1����Q��1��m����ֱ��PQ��x�ᣬy��ֱ���C��D���㣬��M��x��y���Ǹú���ͼ���ϵ�һ�����㣬����M�ֱ���x���y��Ĵ��ߣ�����ֱ�ΪA��B��
��mΪ������m��1��x��0����ͼ����P��m��1����Q��1��m����ֱ��PQ��x�ᣬy��ֱ���C��D���㣬��M��x��y���Ǹú���ͼ���ϵ�һ�����㣬����M�ֱ���x���y��Ĵ��ߣ�����ֱ�ΪA��B��
��1�����OCD�Ķ�����
��2����m=3��1��x��3ʱ�����ڵ�Mʹ����OPM�ס�OCP�����ʱ��M�����ꣻ
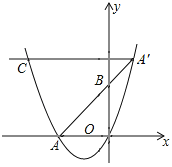
��3����m=5ʱ������OAMB����OPQ���ص����ֵ�����ܷ����4.1����˵��������ɣ�
���𰸡���1����OCD=45�㣻��2��M��2��![]() ������3�������ڣ����ɼ�����.
������3�������ڣ����ɼ�����.
����������1����취֤��OC=OD���ɽ�����⣻
��2����M��a��![]() ��������OPM�ס�OCP���Ƴ�
��������OPM�ס�OCP���Ƴ�![]() ���ɴ˹����������a���ٷ�����⼴�ɽ�����⣻
���ɴ˹����������a���ٷ�����⼴�ɽ�����⣻
��3�������ڷ���������˵�����ٵ�1��x��5ʱ����ͼ1�У��ڵ�x��1ʱ����ͼ2�У��۵�x��5ʱ����ͼ3��.
��1����ֱ��PQ�Ľ���ʽΪy=kx+b������ ![]() ��
��
���![]() ��
��
��y=-x+m+1��
��x=0���õ�y=m+1����D��0��m+1����
��y+0���õ�x=m+1����C��m+1��0����
��OC=OD��
�ߡ�COD=90�㣬
���OCD=45�㣮
��2����M��a��![]() ����
����
�ߡ�OPM�ס�OCP��
��![]() ��
��
��OP2=OCOM��
��m=3ʱ��P��3��1����C��4��0����
OP2=32+12=10��OC=4��OM=![]() ��
��
��![]() ��
��
��10=4![]() ��
��
��4a4-25a2+36=0��
��4a2-9����a2-4��=0��
��a=��![]() ��a=��2��
��a=��2��
��1��a��3��
��a=![]() ��2��
��2��
��a=![]() ʱ��M��
ʱ��M��![]() ��2����
��2����
PM=![]() ��CP=
��CP=![]() ��
��
![]() ������ȥ��
������ȥ��
��a=2ʱ��M��2��![]() ����PM=
����PM=![]() ��CP=
��CP=![]() ��
��
��![]() ��������
��������
��M��2��![]() ����
����
��3�������ڣ��������£�
��m=5ʱ��P��5��1����Q��1��5������M��x��![]() ����
����
OP�Ľ���ʽΪ��y=![]() x��OQ�Ľ���ʽΪy=5x��
x��OQ�Ľ���ʽΪy=5x��
�ٵ�1��x��5ʱ����ͼ1�У�

��E��![]() ��
��![]() ����F��x��
����F��x��![]() x����
x����
S=S����OAMB-S��OAF-S��OBE
=5-![]() x
x![]() x-
x-![]()
![]()
![]() =4.1��
=4.1��
����õ���x4-9x2+25=0��
����O��
��û��ʵ������
�ڵ�x��1ʱ����ͼ2�У�

S=S��OGH��S��OAM=2.5��
����ڣ�
�۵�x��5ʱ����ͼ3�У�

S=S��OTS��S��OBM=2.5��
����ڣ�
���������������ڣ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��6��14������������Ѫ������ij�в�ȡ��Ը�����ķ�ʽ��֯����������Ѫ����ѪʱҪ����Ѫ�ߵ�Ѫ�ͽ��м�⣬���������A��������B��������AB��������O����4�����ͣ�����Ѫ����Ⱥ�У������ȡ�˲�����Ѫ�ߵ�Ѫ�ͽ������ͳ�ƣ����������ͳ�ƽ��������������������ͼ����
Ѫ�� | A | B | AB | O |
���� | �� �� | 10 | 5 | �� �� |
��1����������ȡ����Ѫ������Ϊ�� ���ˣ�m=�� ����
��2����ȫ�ϱ��е����ݣ�
��3������λ�и�����3000��������Ѫ��������ݳ�������ش�
����Ѫ����Ⱥ���γ�ȡһ�ˣ���Ѫ����A�͵ĸ����Ƕ��٣���������3000���д�Լ�ж�������A��Ѫ��

����Ŀ��ij������������Ϊ�˽Ȿ���Ź��˵�������������������˳������飮�ò��������ȡ��30������ij��ÿ�˼ӹ�����ĸ������������£�
20 | 21 | 19 | 16 | 27 | 18 | 31 | 29 | 21 | 22 |
25 | 20 | 19 | 22 | 35 | 33 | 19 | 17 | 18 | 29 |
18 | 35 | 22 | 15 | 18 | 18 | 31 | 31 | 19 | 22 |
�����������ݣ��õ�����ͳ��ͼ��
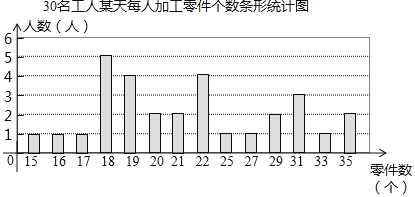
�������ݵ�ƽ��������������λ�����±���ʾ��
ͳ���� | ƽ���� | ���� | ��λ�� |
��ֵ | 23 | m | 21 |
����������Ϣ������������⣺
��1���ϱ�������m��ֵΪ�� ����
��2��Ϊ�������˵Ļ����ԣ��ò��Ÿ��ݹ���ÿ��ӹ�����ĸ����ƶ��˽����������ﵽ��������Ĺ��˽���ý������������һ�����ҵĹ����ܻ�Ӧ������ ����ȷ���������ȽϺ��ʣ�������ƽ����������������������λ������
��3���ò��Ź涨��ÿ��ӹ�����ĸ����ﵽ��25���Ĺ���Ϊ�������֣����ò�����300�����ˣ��Թ��Ƹò����������ֵ�������
����Ŀ�� �����л�ʫ�ʣ�Ѱ�Ļ�����Ʒ����֮������ijУ�ٰ����조�й�ʫ�ʴ�ᡱ����ѡ�κ���50��ѧ���μӾ�������50��ѧ��ͬʱĬд50��ʫ�ʣ���ÿ��ȷĬд��һ��ʫ�ʵ�2�֣����ݲ��Գɼ����Ƴ�����Ƶ���ֲ����Ͳ���Ƶ���ֲ�ֱ��ͼ��ͼ����
����ͼ��������и��⣺
��1��������a��ֵΪ ����λ���ڵ� �飻
��Ƶ���ֲ�ֱ��ͼ����������
��2�������Գɼ�������80��Ϊ���㣬�β��Ե��������Ƕ��٣�
��3����5��10��ͬѧ�У���4����ͬѧ���ֽ���10��ͬѧƽ���ֳ�������жԿ���ϰ����4����ͬѧÿ������ˣ���С����Сǿ������ͬѧ�ܷ���ͬһ��ĸ��ʣ�
��� | �ɼ�x�� | Ƶ���������� |
��1�� | 50��x��60 | 6 |
��2�� | 60��x��70 | 8 |
��3�� | 70��x��80 | 14 |
��4�� | 80��x��90 | a |
��5�� | 90��x��100 | 10 |