题目内容
已知∠AOB=45°，P是它内部的一点，点P关于OA、OB的对称点分别是C和D，则△COD是
- A.锐角三角形
- B.钝角三角形
- C.等边三角形
- D.等腰直角三角形
D
分析：根据轴对称的性质，得OA垂直平分PC，OB垂直平分PD，则OC=OP=OD，则∠COA=∠POA，∠DOB=∠POB，得∠COD=2∠AOB．
解答：∵点P关于OA、OB的对称点分别是C和D，
∴OA垂直平分PC，OB垂直平分PD．
∴OC=OP=OD．
∴∠COA=∠POA，∠DOB=∠POB，
即∠COD=2∠AOB=90°．
故该三角形是等腰直角三角形．
故选D．
点评：此题综合运用了轴对称的性质、等腰三角形的性质和等腰直角三角形的判定．
分析：根据轴对称的性质，得OA垂直平分PC，OB垂直平分PD，则OC=OP=OD，则∠COA=∠POA，∠DOB=∠POB，得∠COD=2∠AOB．
解答：∵点P关于OA、OB的对称点分别是C和D，
∴OA垂直平分PC，OB垂直平分PD．
∴OC=OP=OD．
∴∠COA=∠POA，∠DOB=∠POB，
即∠COD=2∠AOB=90°．
故该三角形是等腰直角三角形．
故选D．
点评：此题综合运用了轴对称的性质、等腰三角形的性质和等腰直角三角形的判定．
练习册系列答案
相关题目
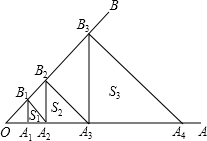如图，已知∠AOB=45°，A1是OA上的一点，且OA1=1，过A1作OA的垂线交OB于点B1，过点B1作OB的垂线交OA于点A2，过点A2作OA的垂线交OB于点B2…，依次记△A1B1A2，△A2B2A3，△A3B3A4…的面积为S1，S2，S3…，则Sn=
如图，已知∠AOB=45°，P为∠AOB内任一点，且OP=5，请在图中分别画出点P关于OA，OB的对称点P1，P2，连P1O，P2O，P1P2，则△OP1P2的面积为
已知∠AOB=45°，P是∠AOB内一点，且PO=4，M、N分别是OA、OB上的动点，则△PMN周长的最小值是
如图，已知∠AOB=45°，A1是OA上的一点，OA1=1，过A1作OA的垂线交OB于点B1，过点B1作OB的垂线交OA于点A2；过A2作OA的垂线交OB于点B2…如此继续，依次记△A1B1A2，△A2B2A3，△A3B3A4…的面积为S1，S2，S3…，则S2011=