Question

园林师老王在两条互相垂直的公路的拐角处承包了一块四边形苗圃地ABCD（如图）他测量后得到如下数据，AB=18米，BC=24米，CD=26米，DA=28米，且∠ABC=90°，请你帮老王计算一下这块苗圃地的面积．

Answer 1

分析：本题要先把解四边形的问题转化成解三角形的问题，再用勾股定理解答．

解答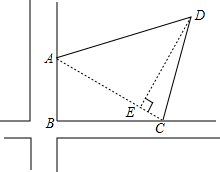：解：连接AC，作DE⊥AC于E点，
∵AB=18米，BC=24米，且∠ABC=90°，
∴AC=

AB2+BC2

=

182+242

=30米，
设EC=x米，则AE=（30-x）米，
∵CD=26米，DA=28米，
∴在Rt△AED和Rt△CED中，AD²-AE²=CD²-CE²，
即：28²-（30-x）²=26²-x²，
解得：x=13.2，
∴DE=

DC2-CE2

=

262-13．22

=22.4米，
∴S_{四边形ABCD}=S_△ABC+S_△ACD
=

1

2

AB•BC+

1

2

AC•DE
=

1

2

×18×24+

1

2

×30×22.4
=216+336
=552平方米．
答：这块苗圃的面积为552平方米．

点评：本题考查了勾股定理的应用，特别是本题中将四边形的面积转化为两个三角形的面积是解题的关键．