题目内容
如图，夜晚在路灯下，一支2m长的标杆AB垂直于地面，它的影子BC=4m，把标杆向左平移到A′B′的位置，此时它的影子刚好是B′B，且B′B=3m．（1）通过画图，在图上找出路灯的位置．
（2）求路灯离地面的高度．
【答案】分析：如图，有AB∥A′B′∥PM，故有△PMC∽△ABC，△PMB∽△A′B′B，所以根据相似三角形的性质建立方程求解．
解答：
解：（1）（3分）如图，点P是路灯的位置．（3分）
（2）过P作PM⊥CB于M（4分）
设PM=x，MB′=y
∵PM∥AB，
∴∠1=∠ABC，∠MPC=∠BAC
∴△PMC∽△ABC
∴
即
①（5分）
同理：△PMB∽△A′B′B
∴
即
②（6分）
解①②联立的方程组得
．（7分）
答：路灯离地面的高度为PM=8米．（8分）
点评：本题利用了相似三角形的性质求解．
解答：
解：（1）（3分）如图，点P是路灯的位置．（3分）（2）过P作PM⊥CB于M（4分）
设PM=x，MB′=y
∵PM∥AB，
∴∠1=∠ABC，∠MPC=∠BAC
∴△PMC∽△ABC
∴
即①（5分）同理：△PMB∽△A′B′B
∴
即②（6分）解①②联立的方程组得
．（7分）答：路灯离地面的高度为PM=8米．（8分）
点评：本题利用了相似三角形的性质求解．
练习册系列答案
相关题目
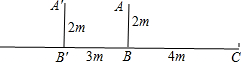的位置，此时它的影子刚好是B′B，且B′B=3m．
