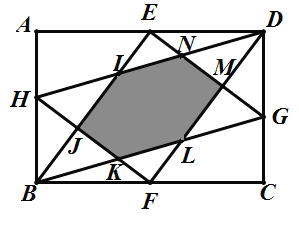
题目内容
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 的中点,
的中点,![]() 分别在
分别在![]() 、
、![]() 上, 且
上, 且![]() ,连结
,连结![]() ,则
,则![]() 与
与![]() 重叠部分六边形
重叠部分六边形![]() 的周长为________
的周长为________
【答案】9.8
【解析】
连结IK,LN,先证出四边形![]() 和四边形
和四边形![]() 是平行四边形,由已知和平行线的性质可得
是平行四边形,由已知和平行线的性质可得![]() 、
、![]() ,由等腰三角形的性质可得
,由等腰三角形的性质可得![]() 互相垂直且平分,进而证得四边形
互相垂直且平分,进而证得四边形![]() 和四边形
和四边形![]() 为菱形,利用相似三角形的性质和线段的计算求出六边形
为菱形,利用相似三角形的性质和线段的计算求出六边形![]() 的各个边长,即可得出周长.
的各个边长,即可得出周长.
解:如图,连结IK,LN,
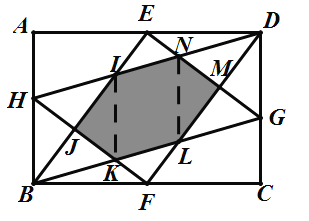
∵四边形![]() 是矩形,
是矩形,![]() ,
,
∴![]() ,
,
∵![]() 分别是
分别是![]() 的中点,
的中点,
∴![]() ,
,![]() ,即
,即![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
由勾股定理得:![]() ,则
,则![]() ,
,
∵![]() ,
,![]() ,则
,则![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,![]() ,
,
∵ ,
,![]() ,即
,即![]() ,
,
又∵![]()
∴![]() ,
,
∴![]() ,
,
同理可得:![]() ,即
,即![]() ,
,
∴四边形![]() 是平行四边形,则
是平行四边形,则![]() ,
,
∴![]() ,
,
∴![]() ,
,
由![]() ,
,![]() 得:
得:![]() 为等腰三角形,
为等腰三角形,
∴![]() 为HK中点,则
为HK中点,则![]() 垂直平分
垂直平分![]() ,
,
又由![]() ,
,![]() 得:
得:![]() 为等腰三角形,
为等腰三角形,
∴![]() 为BI中点,则
为BI中点,则![]() 垂直平分
垂直平分![]() ,
,
则![]() 互相垂直且平分,
互相垂直且平分,
∴四边形![]() 为菱形,
为菱形,![]() ,
,
同理得:四边形![]() 为菱形,
为菱形,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即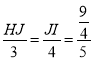 ,
,
解得:![]() ,
,![]() ,
,
∴![]() ,
,
同理得:![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
由勾股定理得:![]() ,
,
∴![]() ,同理得:
,同理得:![]() ,
,
∴六边形![]() 的周长
的周长![]()
![]()
![]()
![]() ,
,
故答案为:![]() .
.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目