题目内容
如图，点P为∠AOB的角平分线上一点，PC⊥OB于点C，PC=2，则点P到OA的距离为________．
2
分析：首先过点P作PD⊥OA于D，由点P为∠AOB的角平分线上一点，PC⊥OB，PC=2，根据角平分线的性质，即可求得点P到OA的距离．
解答：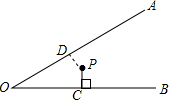
解：过点P作PD⊥OA于D，
∵点P为∠AOB的角平分线上一点，PC⊥OB，PC=2，
∴PD=PC=2，
即点P到OA的距离为2．
故答案为：2．
点评：此题考查了角平分线的性质．此题比较简单，注意掌握角的平分线上的点到角的两边的距离相等定理的应用．
分析：首先过点P作PD⊥OA于D，由点P为∠AOB的角平分线上一点，PC⊥OB，PC=2，根据角平分线的性质，即可求得点P到OA的距离．
解答：
解：过点P作PD⊥OA于D，∵点P为∠AOB的角平分线上一点，PC⊥OB，PC=2，
∴PD=PC=2，
即点P到OA的距离为2．
故答案为：2．
点评：此题考查了角平分线的性质．此题比较简单，注意掌握角的平分线上的点到角的两边的距离相等定理的应用．
练习册系列答案
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
8、如图，点P为∠AOB内一点，分别作点P关于OA，OB的对称点P1，P2，连接P1，P2交OA于M，交OB于N，若P1P2=6，则△PMN周长为（ ）
如图，点P为∠AOB内一点，分别作出P点关于OA、OB的对称点P1，P2，连接P1P2交OA于点M，交OB于点N，P1P2=15，则△PMN的周长为（ ）
如图，点P为∠AOB的角平分线上一点，PC⊥OB于点C，PC=2，则点P到OA的距离为
如图，点P为∠AOB的边OA上的一点，过点P作直线EF∥OB．（要求用尺规作图，不写作法，保留作图痕迹）