题目内容
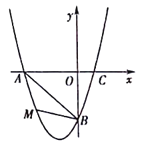
【题目】如图所示，直线y=﹣2x+b与反比例函数y=
交于点A、B，与x轴交于点C．
（1）若A（﹣3，m）、B（1，n）．直接写出不等式﹣2x+b＞的解．
（2）求sin∠OCB的值．
（3）若CB﹣CA=5，求直线AB的解析式．
【答案】（1） x＜﹣3或0＜x＜1；（2）
；（3）y=﹣2x﹣2
．
【解析】
（1）不等式的解即为函数y=﹣2x+b的图象在函数y=
上方的x的取值范围．可由图象直接得到．
（2）用b表示出OC和OF的长度，求出CF的长，进而求出sin∠OCB．
（3）求直线AB的解析式关键是求出b的值．
（1）如图：
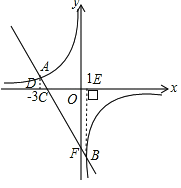
由图象得：不等式﹣2x+b＞的解是x＜﹣3或0＜x＜1；
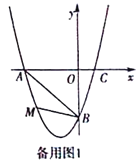
（2）设直线AB和y轴的交点为F．
当y=0时，x=
，即OC=﹣；
当x=0时，y=b，即OF=﹣b，∴CF=
=
，∴sin∠OCB=sin∠OCF=
=
=．
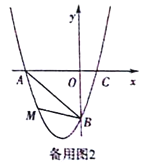
（3）过A作AD⊥x轴，过B作BE⊥x轴，则AC=
AD=
，BC=
，∴AC﹣BC=（yA+yB）=
（xA+xB）
=﹣5，又﹣2x+b=，所以﹣2x2+bx﹣k=0，∴
，∴×
b=﹣5，∴b=
，∴y=﹣2x﹣2．
【题目】为了了解学生关注热点新闻的情况，“两会”期间，小明对班级同学一周内收看“两会”新闻的次数情况作了调查，调查结果统计如图所示（其中男生收看
次的人数没有标出）.
根据上述信息，解答下列各题：
×
（1）该班级女生人数是__________，女生收看“两会”新闻次数的中位数是________；
（2）对于某个群体，我们把一周内收看某热点新闻次数不低于次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低
，试求该班级男生人数；
（3）为进一步分析该班级男、女生收看“两会”新闻次数的特点，小明给出了男生的部分统计量（如表）.
统计量 | 平均数（次） | 中位数（次） | 众数（次） | 方差 | … |
该班级男生 |
|
|
|
| … |
根据你所学过的统计知识，适当计算女生的有关统计量，进而比较该班级男、女生收看“两会”新闻次数的波动大小.
