Question

【题目】在数学中，有许多关系都是在不经意间被发现的．当然，没有敏锐的观察力是做不到的．数学家们往往是这样来研究问题的：特值探究–猜想归纳–逻辑证明–总结应用．下面我们也来像数学家们那样分四步找出这两个代数式的关系：对于代数式与．

特值探究：

当，时，________；________

当，时，________；________

猜想归纳：

观察的结果，写出与的关系：________．

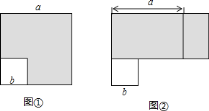
逻辑证明：如图，边长为的正方形纸片剪出一个边长为的小正方形之后，剩余部分（即阴影部分）又剪拼成一个矩形（不重叠无缝隙），请你说说是如何用这个图来得出中的关系？

总结应用：利用你发现的关系，求：

①若，且，则________；

②的值．（提示：你可能要用到公式）

Answer 1

【答案】4；4；16；16；

；

详见解析；

①3；②.

【解析】

把与的值代入两式计算即可得到结果；

归纳总结得出关系即可；

根据阴影部分面积不变，验证即可；

①利用平方差公式计算即可得到结果；

②原式变形后，利用平方差公式计算即可得到结果.

特值探究：

当，时， ，；

当，时， ， ；

猜想归纳：

观察的结果写出与的关系： ；

逻辑证明：

如图，边长为的正方形纸片剪去一个边长为的小正方形之后，剩余部分（即阴影部分）又剪拼成一个矩形（不重叠无缝隙），

左图中阴影部分面积为，右图阴影部分面积为，

故；

总结应用：利用你发现的关系，求：

若，且，则，

原式