��Ŀ����
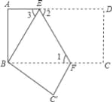
����Ŀ����ƽ��ֱ������ϵ�У��ı���OABCΪ���Σ���A������Ϊ��4��0������B������Ϊ��4��3��������M��N�ֱ��O��Bͬʱ��������ÿ��1����λ���ȵ��ٶ��˶������У���M��OA���յ�A�˶�����N��BC���յ�C�˶�������M��MP��OA����AC��P������NP������˵���ٵ���M�˶���2��ʱ����P������Ϊ��2�� ![]() �����ڵ���M�˶�
�����ڵ���M�˶� ![]() ��ʱ����NPC�ǵ��������Σ��۵���N�˶���2��ʱ����NPC��������ﵽ���ֵ��������ȷ���� ��
��ʱ����NPC�ǵ��������Σ��۵���N�˶���2��ʱ����NPC��������ﵽ���ֵ��������ȷ���� �� 
���𰸡��٢ڢ�
���������⣺A��4��0����C��0��3����
��ֱ��AC�Ľ���ʽΪy=�� ![]() x+3��
x+3��
��t=2ʱ��OM=2��
��x=2ʱ��y=�� ![]() +3=
+3= ![]() ��
��
���P������Ϊ��2�� ![]() �����ʢ���ȷ��
�����ʢ���ȷ��
��t= ![]() ʱ��OM=
ʱ��OM= ![]() ��
��
��CN=4�� ![]() =
= ![]() ��
��
�ӳ�MP��BC��E�����ı���OMEC�Ǿ��Σ�
���CEM=90�㣬
��PE��CN��CE=OM= ![]() ��
��
��CE=EN= ![]() ��
��
��PC=PN��
���PCN�ǵ��������Σ��ʢ���ȷ��
��֪S��PCN= ![]() ��4��t����[3��
��4��t����[3�� ![]() ��4��t��]=��
��4��t��]=�� ![]() ��t��2��2+
��t��2��2+ ![]() ��
��
�ߩ� ![]() ��0��
��0��
��t=2ʱ����PCN�������ʢ���ȷ��
���Դ��Ǣ٢ڢ�

�����㾫����������Ŀ����֪���������þ��ε����ʵ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���վ��ε��ĸ��Ƕ���ֱ�ǣ����εĶԽ�����ȣ�