题目内容
 如图所示,直线AB与x轴交于点A(3,0),与y轴交于点B(0,4),点P为双曲线
如图所示,直线AB与x轴交于点A(3,0),与y轴交于点B(0,4),点P为双曲线 (x>0)上的一点,点P分别作x轴、y轴的垂线段PE、PF,当PE、PF分别与线段AB交于点C、D时.
(x>0)上的一点,点P分别作x轴、y轴的垂线段PE、PF,当PE、PF分别与线段AB交于点C、D时.
(1)AB=______;
(2)AD•BC=______.
解:(1)∵直线AB与x轴交于点A(3,0),与y轴交于点B(0,4),
∴OA=3,OB=4,
∴由勾股定理得AB= =5,;
=5,;
(2):设直线AB的解析式是y=kx+b,
则:
解得:
则直线的解析式是:y=- x+4.
x+4.
设P的坐标是(m, ),在y=-
),在y=- x+4中,令y=
x+4中,令y= ,解得:x=3-
,解得:x=3- ,故D的坐标是(3-
,故D的坐标是(3- ,
, );
);
在y=- x+4中,令x=m,解得:y=4-
x+4中,令x=m,解得:y=4- m,则C的坐标是:(m,4-
m,则C的坐标是:(m,4- m).
m).
则AD= =
= ,
,
BC= =
= m,
m,
则AD•BC= •
• m=
m= .
.
故答案是:5, .
.
分析:(1)直接利用勾股定理求得AB的长即可;
(2)首先求得直线AB的解析式,然后设P的坐标是(m, ),据此即可求得线段AD、BC的长,从而求解.
),据此即可求得线段AD、BC的长,从而求解.
点评:本题考查了待定系数法求函数的解析式,利用数形结合解决此类问题,是非常有效的方法.
∴OA=3,OB=4,
∴由勾股定理得AB=
 =5,;
=5,;(2):设直线AB的解析式是y=kx+b,
则:

解得:
则直线的解析式是:y=-
 x+4.
x+4.设P的坐标是(m,
 ),在y=-
),在y=- x+4中,令y=
x+4中,令y= ,解得:x=3-
,解得:x=3- ,故D的坐标是(3-
,故D的坐标是(3- ,
, );
);在y=-
 x+4中,令x=m,解得:y=4-
x+4中,令x=m,解得:y=4- m,则C的坐标是:(m,4-
m,则C的坐标是:(m,4- m).
m).则AD=
 =
= ,
,BC=
 =
= m,
m,则AD•BC=
 •
• m=
m= .
.故答案是:5,
 .
.分析:(1)直接利用勾股定理求得AB的长即可;
(2)首先求得直线AB的解析式,然后设P的坐标是(m,
 ),据此即可求得线段AD、BC的长,从而求解.
),据此即可求得线段AD、BC的长,从而求解.点评:本题考查了待定系数法求函数的解析式,利用数形结合解决此类问题,是非常有效的方法.

练习册系列答案
相关题目
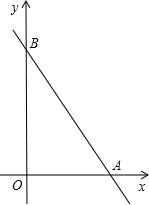 如图所示,直线AB与两坐标轴的交点坐标分别是A(6,0),B(0,8),O是坐标系原点.
如图所示,直线AB与两坐标轴的交点坐标分别是A(6,0),B(0,8),O是坐标系原点.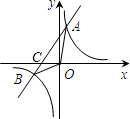 如图所示,直线AB与反比例函数
如图所示,直线AB与反比例函数 如图所示,直线AB与直线CD相交于点O,EO⊥AB,∠EOD=25°,则∠BOD=
如图所示,直线AB与直线CD相交于点O,EO⊥AB,∠EOD=25°,则∠BOD= 如图所示,直线AB与CD相交于O点,∠1=∠2.若∠AOE=140°,则∠AOC 的度数为( )
如图所示,直线AB与CD相交于O点,∠1=∠2.若∠AOE=140°,则∠AOC 的度数为( ) 如图所示,直线AB与CD交于点O,∠BOD=31°36′,OE平分∠BOC,则∠AOD+∠COE=
如图所示,直线AB与CD交于点O,∠BOD=31°36′,OE平分∠BOC,则∠AOD+∠COE=